Trắc nghiệm Toán 10 (có đáp án): Tổng hợp câu hay và khó chương 3 - Phần 3
-
434 lượt thi
-
14 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Phương trình có tích của tát cả các nghiệm nguyên là:
 Xem đáp án
Xem đáp án
Phương trình
Do nên
TH1:
Phương trình
TH2:
Phương trình (do x=4 loại).
Đáp án cần chọn là: B
Câu 2:
Có nhiều nhất bao nhiêu số nguyên m thuộc nửa khoảng để phương trình có nghiệm:
 Xem đáp án
Xem đáp án
Phương trình đã cho tương đương với:
Xét hàm trên ta có
BBT:
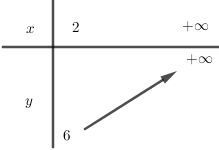
Để phương trình đã cho có nghiệm điều kiện là
Mà suy ra
Vậy có nhiều nhất 2014 số nguyên thỏa mãn yêu cầu bài toán.
Đáp án cần chọn là: A
Câu 3:
Một xe hơi khởi hành từ Krông Năng đi đến Nha Trang cách nhau 175km. Khi về xe tăng vận tốc trung bình hơn vận tốc trung bình lúc đi là 20km/giờ. Biết rằng thời gian dùng để đi và về là 6 giờ; vận tốc trung bình lúc đi là
 Xem đáp án
Xem đáp án
Gọi x, y > 0 (km/giờ)lần lượt là vận tốc trung bình lúc đi và vận tốc trung bình lúc về.
Theo đề bài ta có hệ phương trình:
Thế (1) vào (2) ta được:
vì x>0
Vận tốc lúc đi là 50 km/giờ
Đáp án cần chọn là: D
Câu 4:
Có bao nhiêu giá trị nguyên của m để phương trình có đúng một nghiệm
 Xem đáp án
Xem đáp án
Để phương trình đã cho có đúng một nghiệm thì đường thẳng cắt đồ thị hàm số trên tại một điểm duy nhất.
Lập bảng biến thiên của hàm số trên
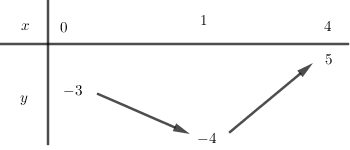
Dựa vào bảng biến thiên ta có:
Để phương trình đã cho có nghiệm duy nhất thuộc th
Vậy các giá trị nguyên của m thỏa mãn là
Đáp án cần chọn là: A
Câu 5:
Cho phương trình . Số các giá trị của m để phương trình có một nghiệm duy nhất?
 Xem đáp án
Xem đáp án
Tập xác định
Phương trình tương đương với
Ta có, phương trình (∗) có:
Phương trình đã cho có duy nhất một nghiệm nếu phương trình (∗) có nghiệm kép
Thay vào phương trình (∗), ta được (thỏa mãn).
Vậy với thì phương trình đã cho có một nghiệm duy nhất.
Đáp án cần chọn là: C
Câu 6:
Khi hệ phương trình có nghiệm với , giá trị là:
 Xem đáp án
Xem đáp án
Kí hiệu
Lấy (1) – (3) vế với vế ta được
Khi đó
Ta có
Đáp án cần chọn là: C
Câu 7:
Cho hệ phương trình có nghiệm là (a; b). Khi đó giá trị biểu thức
 Xem đáp án
Xem đáp án
Điều kiện
Có ta coi (1) là phương trình bậc hai ẩn x và y là tham số, giải x theo y ta được
Với thì (*) (vô lí)
Hệ phương trình có nghiệm là
Đáp án cần chọn là: A
Câu 8:
Cho biết tập hợp tất cả các giá trị của tham số m để phương trình có nghiệm là , với a, b là các số nguyên dương và là phân số tối giản. Tính .
 Xem đáp án
Xem đáp án
Điều kiện xác định: .
Đặt
Phương trình đã cho trở thành
Xét hàm số có bảng biến thiên:
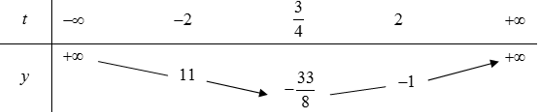
(1) Có nghiệm t thỏa mãn
Vậy T = 3
Đáp án cần chọn là: D
Câu 9:
Các nghiệm của hệ là:
 Xem đáp án
Xem đáp án
Ta có:
Đặt ta được h
Đặt S = u + v, P = uv ta được hệ
hoặc
+ Khi thì u, v là nghiệm của phương trình
+ Khi thì u, v là nghiệm của phương trình (vô nghiệm)
Vậy hệ có nghiệm
Đáp án cần chọn là: A
Câu 10:
Tìm các giá trị của m để phương trình có nghiệm:
 Xem đáp án
Xem đáp án
Phương trình tương đương:
Phương trình (2) có nghiệm <=> pt (2) có ít nhất một nghiệm lớn hơn hoặc bằng –m
Phương trình (2) có nghiệm
Khi đó phương trình (2) có hai nghiệm
Dễ thấy nên (2) luôn có ít nhất 1 nghiệm thỏa mãn bài toán
Vậy
Đáp án cần chọn là: C
Câu 11:
Gọi S là tập hợp tất các giá trị thực của tham số m để đường thẳng cắt parabol tại hai điểm phân biệt A và B sao cho trung điểm I của đoạn thẳng AB thuộc đường thẳng . Tính tổng tất cả các phần tử của S.
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm:
Dễ thấy (1) luôn có 2 nghiệm phân biệt vì
Khi đó (d) cắt (P) tại hai điểm phân biệt , , với là nghiệm phương trình (1). Theo Viét, có:
I là trung điểm
Mà
Đáp án cần chọn là: D
Câu 12:
Cho biết tập hợp tất cả các giá trị của tham số m để phương trình có nghiệm là , với a, b là các số nguyên dương và là phân số tối giản. Tính
 Xem đáp án
Xem đáp án
Đặt khi đó phương trình trở thành
Phương trình có nghiệm khi và chỉ khi phương trình (*) có nghiệm t thỏa mãn
Số nghiệm của phương trình (*) bằng số giao điểm của parabol (P): và đường thẳng
Xét parabol ta có bảng biến thiên như sau:
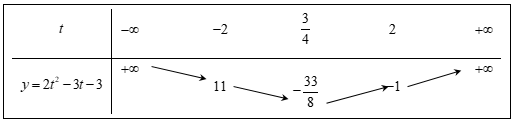
Từ bảng biến thiên ta có phương trình (*) có nghiệm khi và chỉ khi hoặc
Vậy khi thì phương trình có nghiệm
Đáp án cần chọn là: B
Câu 13:
Cho (x,y) với x,y nguyên là nghiệm của hệ phương trình thì tích xy bằng:
 Xem đáp án
Xem đáp án
Điều kiện
Hệ phương trình tương đương với
Từ (1) và x, y là số nguyên nên y là ước của x
Từ (2) ta có x là ước của 12
Vậy có duy nhất một nghiệm nguyên x = 3, y = 1 nên xy = 3
Đáp án cần chọn là: C
Câu 14:
Có bao nhiêu giá trị m nguyên dương để hệ phương trình có nghiệm duy nhất (x,y) sao cho biểu thức nhận giá trị nguyên
 Xem đáp án
Xem đáp án
Ta có nên hệ phương trình luôn có nghiệm duy nhất
Vậy hệ luôn có nghiệm duy nhất là:
Ta có:
Vì m ∈ Z nên để A nguyên thì là ước của 33 mà nên ta có các trường hợp sau:
Mà m nguyên dương nên
Vậy có 2 giá trị nguyên dương của m để A nguyên.
Đáp án cần chọn là: B
