Trắc nghiệm Toán 10 Bài 2. Biểu thức toạ độ của các phép toán vectơ có đáp án
-
219 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho \[\overrightarrow a \] = (2; – 4), \[\overrightarrow b \]= (– 5; 3). Tìm tọa độ của \[\overrightarrow a \] + \[\overrightarrow b \].
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có : \[\overrightarrow a \] + \[\overrightarrow b \] = (2 + (– 5); – 4 + 3) = (– 3; – 1).
Câu 2:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là : A
Ta có : \[\overrightarrow m - \overrightarrow n \] = (3 – (– 1)); – 4 – 2) = (4; – 6).
Câu 3:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là : B
Ta có: 2\[\overrightarrow m \]= 2(–1; 2) = (–2; 4)
2\[\overrightarrow m + \overrightarrow n \] = (– 2 + 5); 4 – 7) = (3; – 3).
Câu 4:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là : A
Tọa độ điểm I là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l}{x_I} = \frac{{ - 1 + 1}}{2} = 0\\{y_I} = \frac{{1 + 1}}{2} = 1\end{array} \right. \Rightarrow I\left( {0;1} \right)\).
Câu 5:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có: 3\[\overrightarrow k \]= 3(5 ; 2) = (15 ; 6) ; 2\[\overrightarrow n \] = 2(10 ; 8) = (20 ; 16)
\[3\overrightarrow k - 2\overrightarrow n \] = (15 – 20 ; 6 – 16) = (– 5; – 10).
Câu 6:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là : B
Ta có \[\left\{ \begin{array}{l}\overrightarrow {AB} = \left( { - 2; - 1} \right)\\\overrightarrow {AC} = \left( { - 3; - 2} \right)\end{array} \right.\] \[ \Rightarrow \]\[\overrightarrow {AB} - \overrightarrow {AC} \] = (– 2 – (– 3); – 1 – (– 2)) = (1; 1).
Câu 7:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là : C
Gọi điểm B có tọa độ (xB ; yB)
Vì I là trung điểm của AB nên ta có :
\[\left\{ \begin{array}{l}{x_I} = \frac{{2 + {x_B}}}{2} = 4\\{y_I} = \frac{{ - 3 + {y_B}}}{2} = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_I} = 2.4 - 2 = 6\\{y_I} = 2.7 - ( - 3) = 17\end{array} \right.\] \[ \Rightarrow \] B(6; 17).
Câu 8:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là : D
Gọi toạ độ trọng tâm G (\[{x_G}\]; \[{y_G}\]), ta có :
\[\left\{ \begin{array}{l}{x_G} = \frac{{3 + 1 + 5}}{3} = 3\\{y_G} = \frac{{5 + 2 + 2}}{3} = 3\end{array} \right.\] \[ \Rightarrow \]G (3; 3).
Câu 9:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là : C
Gọi toạ độ C(x ; y), ta có:
Vì G là trọng tâm tam giác ABC nên : \[\left\{ \begin{array}{l}{x_G} = \frac{{6 + \left( { - 3} \right) + x}}{3} = - 1\\{y_G} = \frac{{1 + 5 + y}}{3} = 1\end{array} \right.\]
\[ \Rightarrow \]\[\left\{ \begin{array}{l}x = - 6\\y = - 3\end{array} \right..\] hay C (–6; –3).
Câu 10:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
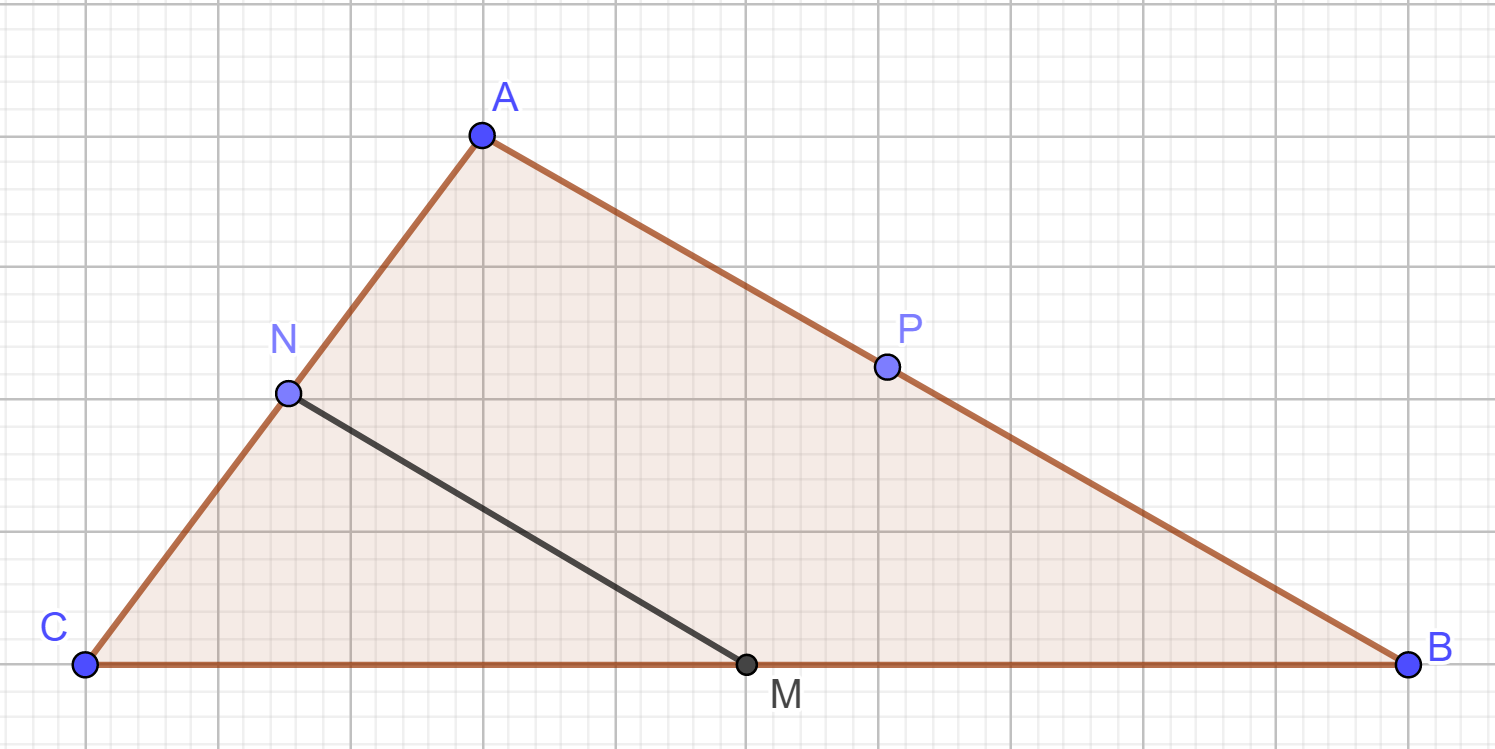
Gọi toạ độ A (x ; y).
Ta có : \[\overrightarrow {PA} \] = (x + 1; y – 6) và \[\overrightarrow {MN} \] = (–2; –7)
Theo tính chất đường trung bình tam giác, ta có:
\[\overrightarrow {MN} \]= \[\frac{1}{2}\]\[\overrightarrow {AB} \] = \[\overrightarrow {PA} \]
Khi đó (1)\[ \Leftrightarrow \]\[\left\{ \begin{array}{l}x + 1 = - 2\\y - 6 = - 7\end{array} \right.\] \[ \Leftrightarrow \]\[\left\{ \begin{array}{l}x = - 3\\y = - 1\end{array} \right.\]
Hay A (–3; –1).
Câu 11:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là : B
Xét tam giác ABC, có :
M là trung điểm AB
N là trung điểm AC
Suy ra MN là đường trung bình tam giác ABC
Theo tính chất đường trung bình, ta có :
\[\overrightarrow {MN} = \frac{1}{2}\overrightarrow {BC} \] = \[\frac{1}{2}\].(2; –8) = (1; –4).
Câu 12:
Trong hệ tọa độ Oxy cho tam giác ABC có C (–2 ; –4), trọng tâm G (0 ; 4) và trung điểm cạnh BC là M (2 ; 0). Tổng hoành độ của điểm A và B là.
Xem đáp án
Hướng dẫn giải
Đáp án đúng là : B
Vì M là trung điểm BC nên ta có : \[\left\{ \begin{array}{l}{x_B} = 2{x_M} - {x_C}\\{y_B} = 2{y_M} - {y_C}\end{array} \right.\]
\[ \Leftrightarrow \]\[\left\{ \begin{array}{l}{x_B} = 2.2 - \left( { - 2} \right) = 6\\{y_B} = 2.0 - \left( { - 4} \right) = 4\end{array} \right.\]\[ \Rightarrow \]B (6; 4).
Vì G là trọng tâm tam giác ABC nên \[\left\{ \begin{array}{l}{x_A} = 3{x_G} - {x_B} - {x_C}\\{y_A} = 3{y_G} - {y_B} - {y_C}\end{array} \right.\]
\[ \Leftrightarrow \]\[\left\{ \begin{array}{l}{x_A} = 3.0 - 6 - ( - 2)\\{y_A} = 3.4 - 4 - ( - 4)\end{array} \right.\]\[ \Leftrightarrow \]\[\left\{ \begin{array}{l}{x_A} = - 4\\{y_A} = 12\end{array} \right.\] hay A (–4 ; 12).
Suy ra \[{x_A} + {x_B}\]= 6 + (–4) = 2.
Câu 13:
Trong hệ tọa độ Oxy cho tam giác ABC có A (– 2 + x ; 2), B (3 ; 5 + 2y), C(x ; 3 – y). Tìm tổng 2x + y với x, y để O (0 ; 0) là trọng tâm tam giác ABC?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là : C
Vì O là trọng tâm tam giác ABC nên, ta có : \[\left\{ \begin{array}{l}{x_G} = \frac{{ - 2 + x + 3 + x}}{3} = 0\\{y_G} = \frac{{2 + 5 + 2y + 3 - y}}{3} = 0\end{array} \right.\]
\[ \Rightarrow \]\[\left\{ \begin{array}{l}x = - \frac{1}{2}\\y = - 10\end{array} \right. \Rightarrow 2.x + y = 2.\left( { - \frac{1}{2}} \right) + \left( { - 10} \right) = - 11\].
Câu 14:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là : C
Gọi toạ độ điểm C (x ; y).
Vì G là trọng tâm tam giác ABC nên ta có : \[\left\{ \begin{array}{l}{x_G} = \frac{{6 + \left( { - 3} \right) + x}}{3} = - 1\\{y_G} = \frac{{1 + 5 + y}}{3} = 1\end{array} \right.\]
\[ \Rightarrow \]\[\left\{ \begin{array}{l}x = - 6\\y = - 3\end{array} \right.\] hay C (–6; –3).
Câu 15:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là : B
Ta có : \[\overrightarrow a - \overrightarrow b \] = (–2m; 2) – (2; –7n) = (–2m –2; 2 + 7n)
Mà \[\overrightarrow a - \overrightarrow b \] = (6; – 5)
Nên ta có: \(\left\{ \begin{array}{l} - 2m - 2 = 6\\2 + 7n = - 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = - 4\\n = - 1\end{array} \right.\)
Vậy m = – 4 và n = – 1.