15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 10 Bài 4. Bất phương trình bậc hai một ẩn có đáp án

Câu 1:

2 x^{2} - 7 x - 15 \geq 0

là:

A. $(- \infty; - \frac{3}{2}] \cup [5; + \infty);$

B. $[- \frac{3}{2}; 5]$

C. $(- \infty; - 5] \cup [\frac{3}{2}; + \infty)$

D. $[- 5; \frac{3}{2}]$

Xem đáp án

Đáp án đúng là : A

Ta có : f(x) = $2 x^{2} - 7 x - 15 = 0 \Leftrightarrow [\begin{array}{l} x = 5 \\ x = - \frac{3}{2} \end{array}$ .

Bảng xét dấu

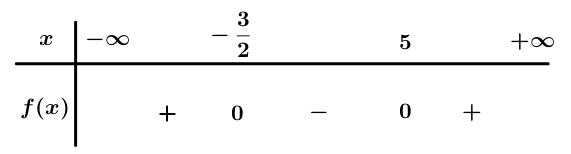
Tập nghiệm của bất phương trình: 2x^2-7x-15 lớn hơn bằng 0 là: (ảnh 1)

Dựa vào bảng xét dấu $2 x^{2} - 7 x - 15 \geq 0 \Leftrightarrow [\begin{array}{l} x \geq 5 \\ x \leq - \frac{3}{2} \end{array} .$

Câu 2:

Tập nghiệm của bất phương trình: $- x^{2} + 6 x + 7 \geq 0$ là:

A. $(- \infty; - 1] \cup [7; + \infty)$

B. $[- 1; 7]$

C. $(- \infty; - 7] \cup [1; + \infty)$

D. $[- 7; 1]$

Xem đáp án

Đáp án đúng là : B

Ta có : f(x) = $- x^{2} + 6 x + 7 = 0 \Leftrightarrow [\begin{array}{l} x = 7 \\ x = - 1 \end{array}$ .

Bảng xét dấu

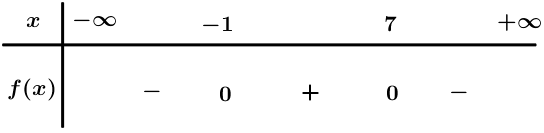
Tập nghiệm của bất phương trình: -x^2+6x+7 lớn hon bằng 0 là: (ảnh 1)

Dựa vào bảng xét dấu $- x^{2} + 6 x + 7 \geq 0 \Leftrightarrow - 1 \leq x \leq 7.$

Câu 3:

Giải bất phương trình $- 2 x^{2} + 3 x - 7 \geq 0.$

B. $S = 0$

B. $S = \{0\};$

C. $S = \emptyset;$

D. $S = ℝ$

Xem đáp án

Đáp án đúng là: C

Ta có : f(x) = $- 2 x^{2} + 3 x - 7 = 0$ vô nghiệm.

Bảng xét dấu

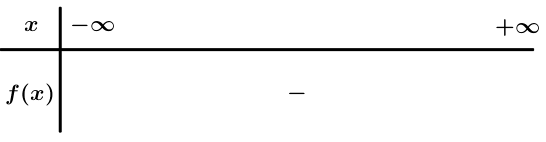
Giải bất phương trình -2x^2+3x-7 lớn hơn bằng 0 (ảnh 1)

Dựa vào bảng xét dấu : $- 2 x^{2} + 3 x - 7 \geq 0 \Leftrightarrow x \in \emptyset$ .

Câu 4:

Tập nghiệm của bất phương trình $x^{2} - 3 x + 2 < 0$ là:

A. $(- \infty; 1) \cup (2; + \infty);$

B. $(2; + \infty);$

C. $(1; 2);$

D. $(- \infty; 1) .$

Xem đáp án

Đáp án đúng là: C

Ta có : $f (x) = x^{2} - 3 x + 2 = 0 \Leftrightarrow [\begin{array}{l} x = 2 \\ x = 1 \end{array}$ .

Bảng xét dấu

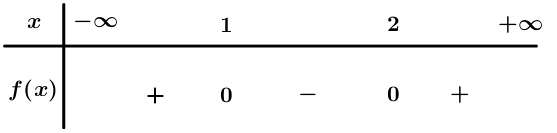
Tập nghiệm của bất phương trình x^2-3x+2<0 là: (ảnh 1)

Dựa vào bảng xét dấu $f (x) < 0 \Leftrightarrow 1 < x < 2$ .

Câu 5:

Tập nghiệm của bất phương trình

- x^{2} + 5 x - 4 < 0

là:

A. $[1; 4]$

B. $(1; 4)$

C. $(- \infty; 1) \cup (4; + \infty)$

D. $(- \infty; 1] \cup [4; + \infty)$

Xem đáp án

Đáp án đúng là: C

Ta có: $f (x) = - x^{2} + 5 x - 4 = 0 \Leftrightarrow [\begin{array}{l} x = 4 \\ x = 1 \end{array}$ .

Bảng xét dấu

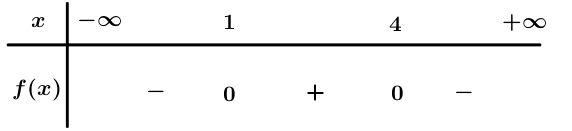
Tập nghiệm của bất phương trình -x^2+ 5x-4<0 là: (ảnh 1)

Dựa vào bảng xét dấu $f (x) < 0 \Leftrightarrow [\begin{array}{l} x < 1 \\ x > 4 \end{array}$ .

Câu 6:

Tập nghiệm của bất phương trình $\sqrt{2} x^{2} - (\sqrt{2} + 1) x + 1 < 0$ là:

A. $(\frac{\sqrt{2}}{2}; 1);$

B. $\emptyset;$

C. $[\frac{\sqrt{2}}{2}; 1];$

D. $(- \infty; \frac{\sqrt{2}}{2}) \cup (1; + \infty) .$

Xem đáp án

Đáp án đúng là: A

Ta có: $f (x) = \sqrt{2} x^{2} - (\sqrt{2} + 1) x + 1 = 0 \Leftrightarrow [\begin{array}{l} x = \frac{\sqrt{2}}{2} \\ x = 1 \end{array}$ .

Bảng xét dấu

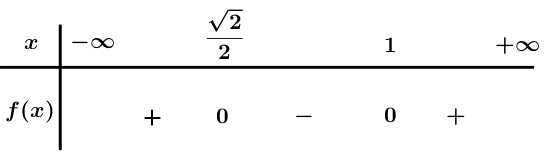
Tập nghiệm của bất phương trình căn bậc hai 2x^2- (căn bậc hai 2+1)x+1<0 là: (ảnh 1)

Dựa vào bảng xét dấu $f (x) < 0 \Leftrightarrow \frac{\sqrt{2}}{2} < x < 1$ .

Câu 7:

Tập nghiệm của bất phương trình $6 x^{2} + x - 1 \leq 0$ là

A. $[- \frac{1}{2}; \frac{1}{3}]$

B. $(- \frac{1}{2}; \frac{1}{3})$

C. $(- \infty; - \frac{1}{2}) \cup (\frac{1}{3}; + \infty)$

D. $(- \infty; - \frac{1}{2}] \cup [\frac{1}{3}; + \infty)$

Xem đáp án

Đáp án đúng là : A

Ta có: $f (x) = 6 x^{2} + x - 1 = 0 \Leftrightarrow [\begin{array}{l} x = \frac{1}{3} \\ x = - \frac{1}{2} \end{array}$ .

Bảng xét dấu

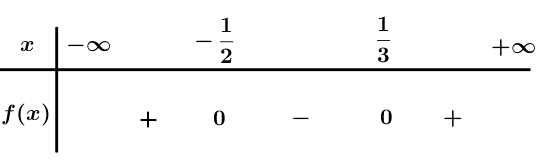
Tập nghiệm của bất phương trình 6x^2+x-1 bé hơn bằng 0 là (ảnh 1)

Dựa vào bảng xét dấu $f (x) \leq 0 \Leftrightarrow - \frac{1}{2} \leq x \leq \frac{1}{3}$ .

Câu 8:

Số thực dương lớn nhất thỏa mãn $x^{2} - x - 12 \leq 0$ là ?

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Đáp án đúng là :D

Ta có $f (x) = x^{2} - x - 12 = 0 \Leftrightarrow [\begin{array}{l} x = 4 \\ x = - 3 \end{array}$ .

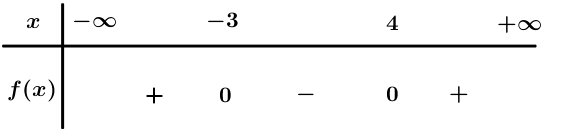
Bảng xét dấu

Số thực dương lớn nhất thỏa mãn x^2 -x-12 bé hơn bằng 0 là ? (ảnh 1)

Dựa vào bảng xét dấu $f (x) \leq 0 \Leftrightarrow - 3 \leq x \leq 4$ . Suy ra số thực dương lớn nhất thỏa $x^{2} - x - 12 \leq 0$ là 4.

Câu 9:

Bất phương trình nào sau đây có tập nghiệm là

ℝ

?

A. $- 3 x^{2} + x - 1 \geq 0;$

B. $- 3 x^{2} + x - 1 > 0;$

C. $- 3 x^{2} + x - 1 < 0;$

D. $- 3 x^{2} + x - 1 \leq 0.$

Xem đáp án

Đáp án đúng là: C

- Xét $f (x) = - 3 x^{2} + x - 1$ có $a = - 3 < 0, Δ = 1^{2} - 4. (- 3) . (- 1) = - 11 < 0$ nên $f (x) < 0, \forall x$ tức là tập nghiệm của bất phương trình là $ℝ$ .

Như vậy chỉ có đáp án C là phù hợp, các đáp án còn lại đều vô nghiệm.

Câu 10:

Cho bất phương trình $x^{2} - 8 x + 7 \geq 0$ . Trong các tập hợp sau đây, tập nào có chứa phần tử không phải là nghiệm của bất phương trình.

A. $(- \infty; 0];$

B. $[8; + \infty);$

C. $(- \infty; 1];$

D. $[6; + \infty) .$

Xem đáp án

Đáp án đúng là: D

Ta có: $f (x) = x^{2} - 8 x + 7 = 0 \Leftrightarrow [\begin{array}{l} x = 1 \\ x = 7 \end{array}$ .

Bảng xét dấu

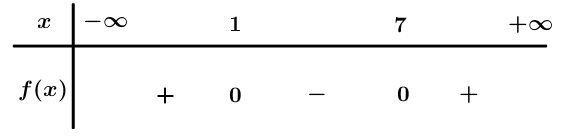
Cho bất phương trình x^2-8x+7 lớn hơn bằng 0. Trong các tập hợp sau đây, tập nào (ảnh 1)

Dựa vào bảng xét dấu $f (x) \geq 0 \Leftrightarrow [\begin{array}{l} x \leq 1 \\ x \geq 7 \end{array}$ .

Tập nghiệm của bất phương trình là $S = (- \infty; 1] \cup [7; + \infty)$ .

Vì $\frac{13}{2} \in [6; + \infty)$ và $\frac{13}{2} \notin S$ nên $[6; + \infty)$ thỏa yêu cầu bài toán.

Câu 11:

Giải bất phương trình $x (x + 5) \leq 2 (x^{2} + 2) .$

A. $x \leq 1;$

B. $1 \leq x \leq 4;$

C. $x \in (- \infty; 1] \cup [4; + \infty);$

D. $x \geq 4.$

Xem đáp án

Đáp án đúng là: C

Bất phương trình $x (x + 5) \leq 2 (x^{2} + 2) \Leftrightarrow x^{2} + 5 x \leq 2 x^{2} + 4 \Leftrightarrow x^{2} - 5 x + 4 \geq 0$

Xét phương trình $x^{2} - 5 x + 4 = 0 \Leftrightarrow (x - 1) (x - 4) = 0 \Leftrightarrow [\begin{array}{l} x = 1 \\ x = 4 \end{array} .$

Lập bảng xét dấu

Dựa vào bảng xét dấu, ta thấy $x^{2} - 5 x + 4 \geq 0 \Leftrightarrow x \in (- \infty; 1] \cup [4; + \infty) .$

Câu 12:

Tập nghiệm S của bất phương trình $x^{2}$ + x - 12 < 0 là:

A. $S = (- 4; 3);$

B. $S = (4; + \infty);$

C. $S = (3; + \infty);$

D. $S = \emptyset .$

Xem đáp án

Đáp án đúng là: A

Tam thức bậc hai f(x) = $x^{2}$ + x - 12 có a = 1 > 0 và có hai nghiệm x = -4; x = 3. Ta có bảng xét dấu:

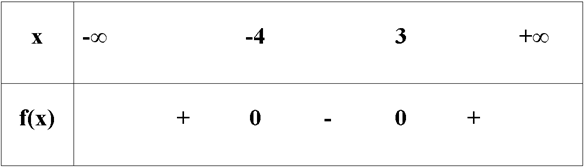
f(x) < 0 suy ra -4 < x < 3.

Câu 13:

Tổng các nghiệm nguyên của bất phương trình $x (2 - x) \geq x (7 - x) - 6 (x - 1)$ trên đoạn $[- 10; 10]$ bằng:

A. 5

B. 6

C. 21

D. 40

Xem đáp án

Đáp án đúng là: D

Bất phương trình:

$x (2 - x) \geq x (7 - x) - 6 (x - 1)$ $\Leftrightarrow 2 x - x^{2} \geq 7 x - x^{2} - 6 x + 6$ $\Leftrightarrow x \geq 6$ . Do x thuộc $[- 10; 10]$ và x nguyên nên ta có: $x \in \{6; 7; 8; 9; 10\}$ .

Tổng các nghiệm nguyên là 6 + 7 + 8 + 9 + 10 = 40.

Câu 14:

Bất phương trình $(2 x - 1) (x + 3) - 3 x + 1 \leq (x - 1) (x + 3) + x^{2} - 5$ có tập nghiệm là:

A. $S = (- \infty; - \frac{2}{3});$

B. $S = [- \frac{2}{3}; + \infty);$

C. $S = ℝ$

D. $S = \emptyset .$

Xem đáp án

Đáp án đúng là: D

Bất phương trình $(2 x - 1) (x + 3) - 3 x + 1 \leq (x - 1) (x + 3) + x^{2} - 5$ tương đương với $2 x^{2} + 5 x - 3 - 3 x + 1 \leq x^{2} + 2 x - 3 + x^{2} - 5$

$0. x \leq - 6 \Leftrightarrow x \in \emptyset$ . Do đó tập nghiệm $S = \emptyset$ .

Câu 15:

Tập nghiệm S của bất phương trình $5 (x + 1) - x (7 - x) > - 2 x$ là:

A. $S = ℝ;$

B. $S = (- \frac{5}{2}; + \infty);$

C. $S = (- \infty; \frac{5}{2});$

D. $S = \emptyset .$

Xem đáp án

Đáp án đúng là: A

Bất phương trình $5 (x + 1) - x (7 - x) > - 2 x$ tương đương với:

$5 x + 5 - 7 x + x^{2} > - 2 x$ $\Leftrightarrow x^{2} + 5 > 0$ . Ta có $x^{2}$ ≥ 0 với mọi $x \in ℝ$ nên $x^{2} + 5 > 0$ đúng với mọi $x \in ℝ$ . Tập nghiệm $S = ℝ$

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Toán 10 Bài 4. Bất phương trình bậc hai một ẩn có đáp án

Trắc nghiệm Toán 10 Bài 4. Bất phương trình bậc hai một ẩn có đáp án

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương