10 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 10 KNTT Bài tập cuối chương 9 (Nhận biết) có đáp án

Câu 1:

Gieo một xúc xắc 2 lần . Biến cố A là biến cố để sau hai lần gieo có ít nhất 1 mặt 6 chấm

A. A = {(1; 6), (2; 6), (3; 6), (4; 6), (5; 6)};

B. A = {(1; 6), (2; 6), (3; 6), (4; 6), (5; 6), (6; 6)};

C. A = {(1; 6), (2; 6), (3; 6), (4; 6), (5; 6), (6; 6), (6; 1), (6; 2), (6; 3), (6; 4), (6; 5)};

D. A = {(6; 1), (6; 2), (6; 3), (6; 4), (6; 5)}.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Biến cố A là biến cố để sau hai lần gieo có ít nhất 1 mặt 6 chấm có 3 trường hợp xảy ra:

Trường hợp 1: lần 1 xuất hiện mặt 6 chấm và lần 2 xuất hiện những mặt còn lại(từ 1 đến 5)

Trường hợp 2 : lần 1 xuất hiện những mặt có số chấm từ 1 đến 5 và lần 2 xuất hiện mặt 6 chấm

Trường hợp 3: 2 lần đều xuất hiện mặt 6 chấm.

Do đó, ta có: A = {(1; 6), (2; 6), (3; 6), (4; 6), (5; 6), (6; 6), (6; 1), (6; 2), (6; 3), (6; 4), (6; 5)}.

Câu 2:

Chọn ngẫu nhiên một số nguyên dương không lớn hơn 15. Hãy mô ta không gian mẫu trên?

A. Ω = {1; 2; 3; 4; 5; 6; 7; 10; 11; 12; 13; 14; 15};

B. Ω = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14};

C. Ω = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14};

D. Ω = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15}.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Ω = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15}.

Câu 3:

Viết tập hợp Ω là không gian mẫu trong trò chơi tung đồng xu hai lần liên tiếp.

A. Ω = {SS; SN; NS; NN};

B. Ω = {SS; SN; NS };

C. Ω = {SS; NS; NN};

D. Ω = {SS; SN; NN}.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Thực hiện tung đồng xu 2 lần có các trường hợp có thể xảy ra là:

TH1: lần 1 đồng xu xuất hiện mặt sấp, lần 2 xuất hiện mặt sấp

TH2: lần 1 đồng xu xuất hiện mặt sấp, lần 2 xuất hiện mặt ngửa

TH3: lần 1 đồng xu xuất hiện mặt ngửa, lần 2 xuất hiện mặt sấp

TH4: lần 1 đồng xu xuất hiện mặt ngửa, lần 2 xuất hiện mặt ngửa

Vậy tập hợp Ω các kêt quả có thể xảy ra là: Ω = {SS; SN; NS; NN}.

Câu 4:

Một lớp có 20 học sinh nam và 18 học sinh nữ. Chọn ngẫu nhiên một học sinh. Xác suất chọn được 1 học sinh nữ là:

A. $\frac{1}{38}$

B. $\frac{10}{19}$

C. $\frac{9}{19}$

D. $\frac{19}{9}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Ta có : Mỗi lần chọn 1 học sinh ngẫu nhiên từ 38 học sinh cho ta một tổ hợp chập 1 của 38 nên n(Ω) = $C_{38}^{1}$ = 38.

Gọi H là biến cố:”học sinh được chọn là học sinh nữ”.

⇒ n(H) = 18.

Vậy P(G) = $\frac{n (H)}{n (Ω)}$ = $\frac{18}{38}$ = $\frac{9}{19}$ .

Câu 5:

Trong các thí nghiệm sau thí nghiệm nào không phải là phép thử ngẫu nhiên:

A. Gieo đồng xu để xem xuất hiện mặt ngửa hay mặt sấp;

B. Gieo đồng xu để xem xuất hiện mặt ngửa xuất hiện bao nhiêu lần;

C. Chọn 1 học sinh bất kì trong lớp và xem kết quả là nam hay nữ;

D. Bỏ hai viên bi xanh và ba viên bi đỏ trong một chiếc hộp, sau đó lấy từng viên một để đếm có tất bao nhiêu viên bi.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Theo định nghĩa ta có phép thử ngẫu nhiên là những phép thử mà ta không thể đoán trước kết quả của nó, mặc dù đã biết được tập hợp tất cả các kết quả của phép thử đó.

Đáp án D không phải phép thử vì ta có thể biết chắc chắn kết quả chỉ có thể là 1 số cụ thể là tổng số bi đỏ và xanh.

Câu 6:

Sắp xếp năm bạn học sinh An; Bình; Chi; Lệ; Dũng vào một chiếc ghế dài có 5 chỗ ngồi. Xác suất để bạn Chi luôn ngồi chính giữa trong năm bạn là:

A. $\frac{1}{5}$

B. $\frac{1}{4}$

C. $\frac{2}{5}$

D. $\frac{3}{4}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Ta có n(Ω) = 5! = 120

Goi R là biến cố “bạn Chi luôn ngồi chính giữa trong năm bạn”

Để bạn Chi ngồi ở giữa chỉ có 1 sự lựa chọn

Số cách xếp 4 bạn sinh An, Bình, Dũng, Lệ vào 4 chỗ còn lại là một hoán vị của 4 phần tử nên có có 4! = 24 cách.

Do đó n(R) = 1.24 = 24 cách xếp.

Vậy P(R) = $\frac{n (R)}{n (Ω)} = \frac{24}{120} = \frac{1}{5}$ .

Câu 7:

Gieo một đồng tiền cân đối ba lần. Các kết quả có thể xảy ra được biểu diễn trong sơ đồ sau:

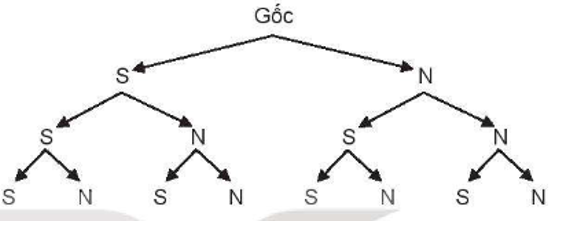
Không gian mẫu là tập:

A. {S; N; S; N; S; N; S; N};

B. {SS; SN; NS; NN};

C. {SSS; SSN; SNS; SNN; NSS; NSN; NNS; NNN};

D. {S; N}.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Dựa vào sơ đồ cây, tập các kết quả của không gian mẫu là:

Ω = {SSS; SSN; SNS; SNN; NSS; NSN; NNS; NNN}.

Câu 8:

Từ các chữ số 1; 2; 4; 6; 8; 9 lấy ngẫu nhiễn một số. Xác suất để lấy được một số nguyên tố là:

A. $\frac{1}{2}$

B. $\frac{1}{3}$

C. $\frac{1}{4}$

D. $\frac{1}{6}$

Xem đáp án

Từ các chữ số 1; 2; 4; 6; 8; 9 lấy ngẫu nhiễn một số. Xác suất để lấy được một số nguyên tố là: (ảnh 1)

Câu 9:

Xác định số phần tử của không gian mẫu các kết quả có thể xảy ra đối với mặt xuất hiện của một xúc xắc sau 3 lần gieo

A. 36;

B. 216;

C. 18;

D. 108.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Ta xem việc thực hiện gieo xúc xắc 3 lần là một công việc gồm 3 giai đoạn:

Giai đoạn 1 : Gieo xúc xắc lần 1: có 6 kết quả có thể xảy ra.

Giai đoạn 2 : Gieo xúc xắc lần 3: có 6 kết quả có thể xảy ra.

Giai đoạn 3 : Gieo xúc xắc lần 3: có 6 kết quả có thể xảy ra.

Do đó, khi thực hiện gieo xúc xắc 3 lần thì có 6.6.6 = 216 có thể xảy ra

Vậy không gian mẫu có 216 phần tử

Câu 10:

Một kệ sách có 3 quyển sách tham khảo Toán, 2 quyển sách tham khảo Văn và 4 quyển sách tham khảo Tiếng Anh. Bạn Hoa lấy ngẫu nhiên 2 quyển sách để học trong ngày hôm nay. Gọi A là biến cố: “Trong 2 quyển sách có 1 quyển sách Toán và 1 quyển sách Tiếng Anh”. Biến P(A) = $\frac{1}{3}$ . Biến cố $\bar{A}$ là gì và có xác suất bằng bao nhiêu?

A. $\bar{A}$ : “Trong 2 quyển sách được chọn không có sách Toán hoặc Tiếng Anh” và P( $\bar{A}$ ) = $\frac{2}{3}$ ;

B. $\bar{A}$ : “Trong 2 quyển sách được chọn không có sách Toán và Tiếng Anh” và P( $\bar{A}$ ) = $\frac{2}{3}$ ;

C. $\bar{A}$ : “Trong 2 quyển sách được chọn không có sách Toán” và P( $\bar{A}$ ) = $\frac{1}{3}$ ;

D.

\bar{A}

: “Trong 2 quyển sách được chọn không có Tiếng Anh” và P(

\bar{A}

) =

\frac{1}{3}

.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

$\bar{A}$ là biến cố đối của biến cố A nên $\bar{A}$ là: “Trong 2 quyển sách được chọn không có sách Toán hoặc Tiếng Anh”.

Khi đó P( $\bar{A}$ ) = 1 – P(A) = 1 – $\frac{1}{3}$ = $\frac{2}{3}$ .

Vậy ta chọn đáp án A.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Toán 10 KNTT Bài tập cuối chương 9 (Phần 2) có đáp án

Trắc nghiệm Toán 10 KNTT Bài tập cuối chương 9 (Nhận biết) có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương