Trắc nghiệm Toán 10 Bài ôn tập cuối chương 8 có đáp án
-
400 lượt thi
-
30 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Tìm số hạng chứa x4 trong khai triển \({\left( {{x^2} - \frac{1}{x}} \right)^n}\) biết \(A_n^2 - C_n^2 = 10\)
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: \(A_n^2 - C_n^2 = 10\)\( \Leftrightarrow \frac{{n!}}{{\left( {n - 2} \right)!}} - \frac{{n!}}{{2!\left( {n - 2} \right)!}} = 10\)
\( \Leftrightarrow \frac{{n(n - 1)(n - 2)...1}}{{(n - 2)...1}} - \frac{{n(n - 1)(n - 2)...1}}{{2.(n - 2)...1}} = 10\)
\( \Leftrightarrow \) n(n – 1) – \(\frac{1}{2}\) n(n – 1) = 10
\( \Leftrightarrow \) \(\frac{1}{2}\)n(n – 1) = 10 \( \Leftrightarrow \) n2 – n – 20 = 0\( \Leftrightarrow \left[ \begin{array}{l}n = 5\\n = - 4\,\end{array} \right.\).
Kết hợp với điều kiện n = 5 thoả mãn
Nhị thức \({\left( {{x^2} - \frac{1}{x}} \right)^n}\)
Ta có công thức số hạng tổng quát trong khai triển (a + b)n là \(C_n^k\)an – k .bk (k ≤ n)
Thay a = x2, b = \( - \frac{1}{x}\) vào trong công thức ta có
\(C_5^k\)(x2)5 – k .\({\left( { - \frac{1}{x}} \right)^k}\) = ( –1)k\(C_5^k\)(x)10 – 3k
Số hạng cần tìm chứa x4 nên ta có 10 – 3k = 4
Vậy k = 2 thoả mãn bài toán
Vậy hệ số của số hạng không chứa x trong khai triển là: ( –1)2\[C_5^2\] = 10
Câu 2:
Từ thành phố A đến thành phố B có 3 con đường, từ thành phố A đến thành phố C có 2 con đường, từ thành phố B đến thành phố D có 2 con đường, từ thành phố C đến thành phố D có 3 con đường, không có con đường nào nối từ thành phố C đến thành phố B. Hỏi có bao nhiêu con đường đi từ thành phố A đến thành phố D.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
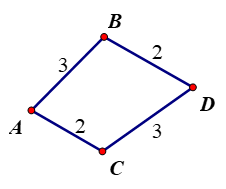
Đi từ thành phố A đến thành phố D ta có các trường hợp sau:
Trường hợp 1. Đi từ thành phố A đến thành phố B rồi đến thành phố D
Ta có: đi là từ thành phố A đến thành phố B có 3 cách, đi là từ thành phố B đến thành phố D có 2 cách
Vậy trường hợp 1 có 3.2 = 6 cách
Trường hợp 2. Đi từ thành phố A đến thành phố C rồi đến thành phố D
Ta có: đi là từ thành phố A đến thành phố C có 2 cách ,đi là từ thành phố C đến thành phố D có 3 cách
Vậy trường hợp 2 có 2.3 = 6 cách
Để đi từ thành phố A đến thành phố D ta có 6 + 6 = 12 cách.
Câu 3:
Cho các số 1; 2; 3; 4; 5 có thể lập được bao nhiêu số tự nhiên lẻ gồm 3 chữ số đôi một khác nhau và chia hết cho 3.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Gọi số cần lập \(\overline {abc} \), a ≠ 0.
Trường hợp 1: c = 1
Số a, b được lập từ các cặp số sau: {2; 3}; {3; 5}. Mỗi cặp lập được 2 số nên có 2.2 = 4 số
Trường hợp 2: c = 3
Số a, b được lập từ các cặp số sau: {1; 2}; {1; 5}; {2; 4}; {4; 5}. Mỗi cặp số lập được 2 số nên có 4.2 = 8 số
Trường hợp 3: c = 5
Số a, b được lập từ các cặp số sau: {1; 3}; {3; 4}. Mỗi cặp số lập được 2 số nên có 2.2 = 4 số
Số các số tự nhiên lẻ gồm 3 chữ số đôi một khác nhau và chia hết cho 3 là: 3 + 8 + 4 = 15 (số)
Câu 4:
Có 10 quả cầu đỏ được đánh số từ 1 đến 10, 7 quả cầu xanh được đánh số từ 1 đến 7 và 8 quả cầu vàng được đánh số từ 1 đến 8. Hỏi có bao nhiêu cách lấy ra 3 quả cầu khác màu và khác số.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta chọn các quả cầu theo trình tự sau:
Công đoạn 1, Chọn quả cầu xanh: 7 cách chọn (Vì cầu xanh được chọn tuỳ ý từ 1 đến 7)
Công đoạn 2, Chọn quả cầu vàng: có 7 cách chọn (Vì số đánh trên cầu vàng không được chọn lại số đã đánh trên quả cầu xanh đã chọn)
Công đoạn 3, Chọn quả cầu đỏ: có 8 cách chọn (Vì số trên quả cầu đỏ chọn không được chọn lại các số mà quả cầu xanh và quả cầu vàng đã chọn)
Tổng kết, số cách lấy ra 3 quả cầu khác màu và khác số là 7.7.8 = 392 cách chọn
Câu 5:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
chọn học sinh nam có 15 cách
chọn học sinh nữ có 25 cách
Tổng kết, áp dụng quy tắc nhân có 15.25 = 375 (cách chọn)
Câu 6:
Trong khai triển nhị thức (x + 2y)3 có bao nhiêu số hạng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Trong khai triển nhị thức (a + b)n có n + 1 số hạng.
Vậy trong khai triển nhị thức (x + 2y)3 có 4 số hạng.
Câu 7:
Trong một hộp có 7 viên bi đỏ, 5 viên bi trắng và 6 viên bi xanh. Chọn ngẫu nhiên ra 4 viên bi. Có bao nhiêu cách để chọn được 2 viên bi xanh.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Vì chọn ngẫu nhiên 4 viên bi và có 2 bi xanh nên ta có các trường hợp sau
Trường hợp 1: chọn được 2 bi xanh, 2 bi đỏ và 0 bi trắng
Số cách chọn là: \(C_6^2.C_7^2.C_5^0 = 315\)
Trường hợp 2: Chọn được 2 bi xanh, 2 bi trắng, 0 bi đỏ
Số cách chọn là: \(C_6^2.C_7^0.C_5^2 = 150\)
Trường hợp 3: Chọn được 2 bi xanh, 1 bi trắng, 1 bi đỏ
Số cách chọn là: \(C_6^2.C_7^1.C_5^1 = 525\)
Áp dụng quy tắc cộng ta có: 315 + 150 + 525 = 990
Câu 8:
Nếu một đa giác đều có 44 đường chéo, thì số cạnh của đa giác là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Cứ hai đỉnh của đa giác n (n ≥ 3, n \( \in \) ℕ) đỉnh tạo thành một đoạn thẳng (bao gồn cả cạnh đa giác và đường chéo).
Khi đó số đường chéo là: \(C_n^2 - n\)
Theo giả thiết ta có: \(C_n^2 - n = 44 \Leftrightarrow \frac{{n!}}{{\left( {n - 2} \right)!.2!}} - n = 44\)
\( \Leftrightarrow \) n(n – 1) – 2n = 88
\( \Leftrightarrow \)n = 11 hoặc n = – 8.
Kết hợp với điều kiện n = 11 thoả mãn.
Câu 9:
Một tổ gồm 7 nam và 6 nữ. Hỏi có bao nhiêu cách chọn 4 em đi trực sao cho có ít nhất 2 nữ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Vì chọn ra 4 học sinh trong đó có ít nhất hai nữ ta có các trường hợp sau
Trường hợp 1: Chọn được 2 nữ và 2 nam
Số cách chọn là: \(C_7^2.C_6^2\) = 315
Trường hợp 2: Chọn được 3 nữ và 1 nam
Số cách chọn là: \(C_7^3.C_6^1\) = 210
Trường hợp 3: Chọn được 4 nữ và 0 nam
Số cách chọn là: \(C_7^4.C_6^0\) = 35
Áp dụng quy tắc cộng ta có: 315 + 210 + 35 = 560 cách.
Câu 10:
Trong khai triển (x2 – 2x)5 hệ số của số hạng chứa x6 là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có công thức số hạng tổng quát trong khai triển (a + b)n là \(C_n^k\)an – k .bk (k ≤ n)
Thay a = x2, b = – 2x vào trong công thức ta có
\(C_5^k\)(x2)5 – k .(– 2x)k = (– 2)k\(C_5^k\) (x)10 – k
Số hạng cần tìm chứa x6 nên ta có 10 – k = 6
Do đó k = 4 thoả mãn bài toán
Khi đó hệ số cần tìm là (– 2)4\(C_5^4\) = 80.Câu 11:
Biết giá trị của n thoả mãn \[A_n^3 = 56n\] tính giá trị của biểu thức P = \(3n + C_{n + 2}^4\)
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Điều kiện n ≥ 3, n \( \in \)ℕ.
\[A_n^3 = 56n\]\[ \Leftrightarrow \frac{{n!}}{{\left( {n - 3} \right)!}} = 56n\]
\[ \Leftrightarrow \frac{{n(n - 1)(n - 2)(n - 3)...1}}{{(n - 3)...1}} = 56n\]
\( \Leftrightarrow \) n(n – 1)(n – 2) = 56n
\( \Leftrightarrow \) n2 – 3n – 54 = 0 \( \Leftrightarrow \left[ \begin{array}{l}n = 9\\n = - 6\end{array} \right.\)
Kết hợp với điều kiện n = 9 thoả mãn bài toán
Giá trị của biểu thức P = \(3n + C_{n + 2}^4\) = 3.9 + \(C_{11}^4\) = 357.
Câu 12:
An muốn qua nhà Bình để cùng Bình đến chơi nhà Cường. Từ nhà An đến nhà Bình có 4 con đường đi, từ nhà Bình đến nhà Cường có 6 con đường đi. Hỏi An có bao nhiêu cách chọn đường đi đến nhà Cường?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Từ nhà An đến nhà Bình có 4 cách chọn đường.
Từ nhà Bình đến nhà Cường có 6 cách chọn đường.
Áp dụng quy tắc nhân ta có số cách chọn đường đi từ nhà An đến nhà Cường là: 4.6 = 24 (cách).
Câu 13:
Biến n là số nguyên dương thỏa mãn \(A_n^3 + 2A_n^2 = 100\). Hệ số của x5 trong khai triển (1 – 3x)n bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
ĐK: n ≥ 3; n \( \in \) ℕ.
Ta có: \(A_n^3 + 2A_n^2 = 100\)
\( \Leftrightarrow \) \(\frac{{n!}}{{\left( {n - 3} \right)!}} + 2.\frac{{n!}}{{\left( {n - 2} \right)!}} = 100\)\( \Leftrightarrow \) \(\frac{{n\left( {n - 1} \right)\left( {n - 2} \right)\left( {n - 3} \right)!}}{{\left( {n - 3} \right)!}} + 2.\frac{{n\left( {n - 1} \right)\left( {n - 2} \right)!}}{{\left( {n - 2} \right)!}} = 100\)
\( \Leftrightarrow \)n(n – 1)(n – 2) + 2n(n – 1) = 100 \( \Leftrightarrow \)n3 – n2 – 100 = 0\( \Leftrightarrow \)n = 5
Khi đó: \({\left( {1 - 3x} \right)^n} = {\left( {1 - 3x} \right)^5}\)
Ta có số hạng tổng quát trong khai triển nhị thức (a + b)n là \(C_n^k\)an - kbk
Thay a = 1 , b = – 3x vào công thức ta có
\(C_5^k\)15-k (– 3x)k = – 3k\(C_5^k\)xk
Cần tìm hệ số của x5 nên ta có k = 5
Hệ số cần tìm là : – 35\(C_5^5\) = – 243.
Câu 14:
Từ các chữ số 0; 1; 2; 3; 4; 5; 6 có thể lập được bao nhiêu số tự nhiên chẵn có ba chữ số khác nhau?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Gọi số có ba chữ số cần tìm là \[\overline {abc} \], với a ≠ 0
Trường hợp 1: c = 0
Chọn số c có 1cách
Chọn số a có 6 cách (vì a ≠ 0 nên a có thể chọn một trong 6 số là 1; 2; 3; 4; 5; 6)
Chọn số b có 5 cách (vì b ≠ a, b ≠ c nên b còn 5 cách chọn)
Vậy có 6.5.1 = 30 số
Trường hợp 2: c ≠ 0
Chọn c có 3 cách chọn (vì số \[\overline {abc} \] là số chẵn nên c có thể chọn một trong 3 số là 2; 4; 6)
Chọn số a có 5 cách chọn (vì a ≠ 0 và a ≠ c nên a có 5 cách chọn)
Chọn số b có 5 cách chọn(vì b ≠ a, b ≠ c nên b còn 5 cách chọn)
Vậy có 5.5.3 = 75 số
Số các số tự nhiên chẵn có 3 chữ số khác nhau lập từ các số trên là: 75 + 30 = 105.
Câu 15:
Bạn Dũng có 9 quyển truyện tranh khác nhau và 6 quyển tiểu thuyết khác nhau. Bạn Dũng có bao nhiêu cách chọn ra một quyển sách để đọc vào cuối tuần.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Sách bạn Dũng có thể lấy ra thuộc hai loại: Truyện tranh hoặc tiểu thuyết.
Truyện tranh: 9 quyển
Tiểu thuyết: 6 quyển
Số cách Dũng lấy ra một quyển là: 9 + 6 = 15 (cách).
Câu 16:
Hệ số của x3y3 trong khai triển nhị thức (1 + x)5(1 + y)5 là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có hệ số của x3 có khai triển (1 + x)5 là
Ta có công thức số hạng tổng quát trong khai triển (a + b)n là \(C_n^k\)an – k .bk (k ≤ n)
Thay a = 1, b = x vào trong công thức ta có \(C_5^k\)15 – k .(x)k = \(C_5^k\)15 – k .(x)k
Vì tìm hệ số của x3 nên ta có xk = x3 \( \Rightarrow \) k = 3
Hệ số của x3 trong khai triển (1 + x)5 là \(C_5^3\).13 = 10.
Ta có hệ số của y3 có khai triển (1 + y)6 là
Ta có công thức số hạng tổng quát trong khai triển (a + b)n là \(C_n^k\)an – k .bk (k ≤ n)
Thay a = 1, b = y vào trong công thức ta có \(C_5^k\)15 – k .(y)k = \(C_5^k\)15 – k .(y)k
Vì tìm hệ số của y3 nên ta có yk = y3 \( \Rightarrow \) k = 3
Hệ số của y3 trong khai triển (1 + y)5 là \(C_5^3\).13 = 10
Hệ số của x3y3 trong khai triển nhị thức (1 + x)5(1 + y)5 là: 10.10 = 100.
Câu 17:
Cho các số 0; 1; 2; 3; 4; 5; 6; 7 có thể lập được bao nhiêu số tự nhiên lẻ gồm 4 chữ số đôi một khác nhau
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Gọi số cần lập \(\overline {abcd} \), a ≠ 0.
chọn số d có 4 cách chọn (Vì \(\overline {abcd} \) là số lẻ nên d chỉ có thể chọn một trong 4 số 1; 3; 5; 7)
chọn số a có 6 cách chọn (Vì a ≠ 0; a ≠ d nên a không được chọn số 0 và số d đã chọn)
chọn số b có 6 cách chọn (Vì b ≠ a; b ≠ d nên b không được chọn lại số a, d đã chọn)
chọn số c có 5 cách chọn (Vì c ≠ a; c ≠ b; c ≠ d nên c không được chọn lại số a, b, d đã chọn)
áp dụng quy tắc nhân ta có số các số tự nhiên lẻ gồm 4 chữ số đôi một khác nhau là: 4.6.6.5 = 720.
Câu 18:
Trong khai triển (x – 2y)4 số hạng chứa x2y2 là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có công thức số hạng tổng quát trong khai triển (a + b)n là \(C_n^k\)an – k .bk (k ≤ n)
Thay a = x, b = – 2y vào trong công thức ta có
\(C_2^k\)(x)4 – k .(– 2y)k = (– 2)k\(C_2^k\) (x)4 – k .(y)k
Số hạng cần tìm chứa x2y2 nên ta có x4 – kyk = x2y2
Vậy k = 2 thoả mãn bài toán
Khi đó hệ số cần tìm là (– 2)2\(C_4^2\) = 24.
Câu 19:
Trong khai triển \[{\left( {x + \frac{8}{{{x^2}}}} \right)^5}\] số hạng chứa x2 là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có \[{\left( {x + \frac{8}{{{x^2}}}} \right)^5}\]
Ta có công thức số hạng tổng quát trong khai triển (a + b)n là \(C_n^k\)an – k .bk (k ≤ n)
Thay a = x, b = \(\frac{8}{{{x^2}}}\) vào trong công thức ta có
\(C_5^k\)(x)5 – k \({\left( {\frac{8}{{{x^2}}}} \right)^k}\)= 8k\(C_5^k\)(x)5 – k \({\left( {\frac{1}{{{x^2}}}} \right)^k}\)= 8k\(C_5^k\) x5 - 3k
Số hạng cần tìm chứa x2 nên ta có 5 – 3k = 2
Do đó k = 1 thoả mãn bài toán
Khi đó hệ số cần tìm là (8)1\(C_5^1\) = 40.
Vậy số hạn cần tìm là 40x2.
Câu 20:
Trong khai triển nhị thức \({\left( {2{x^2} + \frac{1}{x}} \right)^n}\) hệ số của x3 là \({2^2}C_n^1\) Giá trị của n là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Khai triển nhị thức
Ta có công thức số hạng tổng quát trong khai triển (a + b)n là \(C_n^k\)an – k .bk (k ≤ n)
Thay a = 2x2, b = \(\frac{1}{x}\) vào trong công thức ta có
\(C_n^k\)(2x2)n – k \({\left( {\frac{1}{x}} \right)^k}\)= (2)n-k\(C_n^k\)(x)2n –3k
Vì hệ số của số hạng chứa x3 là \({2^2}C_n^1\) nên ta có k = 1
Số hạng cần tìm chứa x3 nên ta có 2n – 3.1 = 3
Vậy n = 3 thoả mãn bài toán
Câu 21:
Biết hệ số của x3 trong khai triển của (1 – 3x)n là – 270. Giá trị của n là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có công thức số hạng tổng quát trong khai triển (a + b)n là \(C_n^k\)an – k .bk (k ≤ n)
Thay a = 1, b = – 3x vào trong công thức ta có
\(C_n^k\)(1)n – k .(– 3x)k = (– 3)k(1)n-k\(C_n^k\)(x)k
Số hạng cần tìm chứa x3 nên ta có k = 3
Vậy k = 3 thoả mãn bài toán
Vì hệ số chứa x3 bằng – 270 nên
(– 3)3(1)n-3\(C_n^3\) = – 270 \( \Leftrightarrow \) \[C_n^3 = 10\]
\( \Leftrightarrow \frac{{n!}}{{3!(n - 3)!}} = \frac{{n(n - 1)(n - 2)\left( {n - 3} \right)...1}}{{6(n - 3)\left( {n - 4} \right)...1}} = 10\)
\( \Leftrightarrow \frac{{n(n - 1)\left( {n - 2} \right)}}{6} = 10\) \( \Leftrightarrow \) n3 – 3n2 + 2n – 60 = 0 \( \Leftrightarrow \) (n – 5)(n2 + 2n + 12) = 0\( \Leftrightarrow n = 5\)
Kết hợp với điều kiện n = 5 thoả mãn bài toán
Câu 22:
Có bao nhiêu số tự nhiên có 6 chữ số đôi một khác nhau trong đó chứa các chữ số 3, 4, 5 và chữ số 4 đứng cạnh chữ số 3 và chữ số 5?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Giả sử mỗi số thỏa mãn yêu cầu bài toán có dạng \(\overline {abcdef} \).
Ta thấy các chữ số 3, 4, 5 luôn đứng cạnh nhau và chữ số 4 đứng giữa hai chữ số còn lại.
Trường hợp 1: b = 4 vậy a và c phải bằng 3 hoặc 5
Chọn d có 7 cách chọn(vì d có thể chọn một trong các số từ 0 đến 9 bỏ đi số 3, 4, 5)
Chọn e có 6 cách chọn(vì e có thể chọn một trong các số từ 0 đến 9 bỏ đi số 3, 4, 5 và số d đã chọn)
Chọn f có 5 cách chọn(vì f có thể chọn một trong các số từ 0 đến 9 bỏ đi số 3, 4, 5 và số d, e đã chọn)
Vậy có 2.7.6.5 = 420 số
Trường hợp 2: c bằng 4 vậy b và d phải bằng 3 hoặc 5
Chọn a có 6 cách (vì a có thể chọn một trong các số từ 1 đến 9 bỏ đi số 3, 4, 5)
Chọn e có 6 cách (vì e có thể chọn một trong các số từ 0 đến 9 bỏ đi số 3, 4, 5 và số a đã chọn)
Chọn f có 5 cách (vì f có thể chọn một trong các số từ 0 đến 9 bỏ đi số 3, 4, 5 và số a, e đã chọn)
Vậy có 6.2.6.5 = 360 số
Trường hợp 3: d bằng 4 vậy c và e phải bằng 3 hoặc 5
Chọn a có 6 cách (vì a có thể chọn một trong các số từ 1 đến 9 bỏ đi số 3, 4, 5)
Chọn b có 6 cách (vì b có thể chọn một trong các số từ 0 đến 9 bỏ đi số 3, 4, 5 và số a đã chọn)
Chọn f có 5 cách (vì f có thể chọn một trong các số từ 0 đến 9 bỏ đi số 3, 4, 5 và số a, e đã chọn)
Vậy có 6.2.6.5 = 360 số
Trường hợp 4: e bằng 4 vậy d và f phải bằng 3 hoặc 5
Chọn a có 6 cách (vì a có thể chọn một trong các số từ 1 đến 9 bỏ đi số 3, 4, 5)
Chọn b có 6 cách (vì b có thể chọn một trong các số từ 0 đến 9 bỏ đi số 3, 4, 5 và số a đã chọn)
Chọn c có 5 cách (vì c có thể chọn một trong các số từ 0 đến 9 bỏ đi số 3, 4, 5 và số a, b đã chọn)
Vậy có 6.2.6.5 = 360 số
Áp dụng quy tắc cộng ta có: 420 + 360 + 360 + 360 = 1500 số
Câu 23:
Một lớp học có 30 bạn học sinh trong đó có 3 cán sự lớp. Hỏi có bao nhiêu cách cử 4 bạn học sinh đi dự đại hội đoàn trường sao cho trong 4 học sinh đó có ít nhất 1 cán sự lớp.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Số cách cử 4 bạn học sinh trong 30 bạn là: \[C_{30}^4 = 27405\].
Số cách cử 4 bạn học sinh trong 27 bạn trong đó không có cán sự lớp là: \[C_{27}^4 = 17550\]Vậy số cách cử 4 bạn học sinh trong đó có ít nhất 1 cán sự lớp là: 27405 – 17550 = 9855.
Câu 24:
Có 10 đội bóng thi đấu theo thể thức vòng tròn một lượt, thắng được 3 điểm, hòa 1 điểm, thua 0 điểm. Kết thúc giải đấu, tổng cộng số điểm của tất cả 10 đội là 130. Hỏi có bao nhiêu trận hòa ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vì 10 đội bóng thi đấu theo thể thức vòng tròn một lượt nên số trận đấu là \(C_{10}^2 = 45\) (trận).
Gọi số trận hòa là x, số không hòa là 45 – x (trận).
Tổng số điểm mỗi trận hòa là 2, tổng số điểm của trận không hòa là 3(45 – x).
Theo đề bài ta có phương trình 2x + 3(45 – x) = 130 \( \Leftrightarrow \) x = 5.
Vậy có 5 trận hòa.
Câu 25:
Trong kho đèn trang trí đang còn 5 bóng đèn loại I, 7 bóng đèn loại II, các bóng đèn đều khác nhau về màu sắc và hình dáng. Lấy ra 5 bóng đèn bất kỳ. Hỏi có bao nhiêu khả năng xảy ra số bóng đèn loại I nhiều hơn số bóng đèn loại II?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Lấy ra 5 bóng đèn bất kỳ thoả mãn bóng đèn loại I nhiều hơn bóng đèn loại II nên ta có các trường hợp sau:
Trường hợp 1: Lấy được 5 bóng đèn loại I: có \(C_5^5\) = 1 cách
Trường hợp 2: Lấy được 4 bóng đèn loại I, 1 bóng đèn loại II: có \(C_5^4.C_7^1\) = 35 cách
Trường hợp 3: Lấy được 3 bóng đèn loại I, 1 bóng đèn loại II: có \(C_5^3.C_7^2\) = 210 cách
Theo quy tắc cộng, có 1 + 35 + 210 = 246 cách.
Câu 26:
Tính giá trị \[M = A_{n - 15}^2 + 3A_{n - 14}^3\], biết rằng \[C_n^4 = 20C_n^2\]
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Điều kiện n ≥ 17; n \( \in \) ℕ, ta có \[C_n^4 = 20C_n^2\]\[ \Leftrightarrow \frac{{n!}}{{4!\left( {n - 4} \right)!}} = 20\frac{{n!}}{{2!\left( {n - 2} \right)!}}\]
\( \Leftrightarrow \) (n – 2)(n – 3) = 240\[ \Rightarrow \left[ \begin{array}{l}n = 18\\n = - 13\end{array} \right.\]
Kết hợp với điều kiện n = 18 thoả mãn. Vậy \[M = A_3^2 + 3A_4^3\] = 78.
Câu 27:
Cho số tự nhiên n thỏa mãn \(3C_{n + 1}^3 - 3A_n^2 = 42\left( {n - 1} \right)\). Giá trị của biểu thức \(3C_n^4 - A_n^2\) là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Điều kiện n \( \in \)ℕ, n ≥ 2.
Ta có \(3C_{n + 1}^3 - 3A_n^2 = 42\left( {n - 1} \right)\)\( \Leftrightarrow 3\frac{{\left( {n + 1} \right)!}}{{3!\left( {n - 2} \right)!}} - 3\frac{{n!}}{{\left( {n - 2} \right)!}} = 42\left( {n - 1} \right)\)
\( \Leftrightarrow 3\frac{{(n + 1)n(n - 1)(n - 2)...1}}{{3.2.1.(n - 2)...1}} - 3\frac{{n(n - 1)(n - 2)...1}}{{(n - 2)(n - 3)...1}} = 42(n - 1)\)
\( \Leftrightarrow \frac{{\left( {n + 1} \right)n\left( {n - 1} \right)}}{2} - 3n\left( {n - 1} \right) = 42\left( {n - 1} \right)\)
\( \Leftrightarrow \) (n + 1)n – 6n = 84
\( \Leftrightarrow \) n2 – 5n – 84 = 0
\( \Leftrightarrow \left[ \begin{array}{l}n = 12\\n = - 7\end{array} \right.\)
Kết hợp điều kiện ta có n = 12 thoả mãn điều kiện đầu bài.
Giá trị của biểu thức \(3C_n^4 - A_n^2\) = \(3C_{12}^4 - A_{12}^2\) =1353.
Câu 28:
Cho tập A gồm n điểm phân biệt trên mặt phẳng sao cho không có 3 điểm nào thẳng hàng. Tìm n sao cho số tam giác có 3 đỉnh lấy từ 3 điểm thuộc A gấp đôi số đoạn thẳng được nối từ 2 điểm thuộc A.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Theo đề bài: Vì trong tập A không có 3 điểm nào thẳng hàng nên lấy bất kỳ 3 điểm của tập A sẽ tạo thành một tam giác và lấy 2 điểm bất kì của tập A sẽ tạo thành một đoạn thẳng. Số tam giác lập được là \(C_n^3\), số đoạn thẳng có thể tạo thành là \(C_n^2\). Theo bài ra ta có \(C_n^3 = 2C_n^2\) (1) (với n \( \in \)ℕ, n ≥ 3)
\[ \Leftrightarrow \frac{{n!}}{{3!\left( {n - 3} \right)!}} = 2\frac{{n!}}{{2!\left( {n - 2} \right)!}} \Leftrightarrow \frac{1}{6} = \frac{1}{{n - 2}} \Leftrightarrow n = 8\].
Câu 29:
Cho các chữ số 2, 3, 4, 5, 6, 7, 8, 9 số các số tự nhiên chẵn có 3 chữ số lập thành từ các chữ số đã cho là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Gọi số tự nhiên có 3 chữ số cần tìm là: \[\overline {abc} \] (a ≠ 0) khi đó
chọn số c có 4 cách chọn ( vì \[\overline {abc} \] là số chẵn nên c chỉ có thể chọn một trong các số 2, 4, 6, 8)
chọn số a có 8 cách chọn (vì a được chọn tuỳ ý nên a có thể chọn một trong 8 số 2, 3, 4, 5, 6, 7, 8, 9)
chọn số b có 8 cách chọn (vì b được chọn tuỳ ý nên b có thể chọn một trong 8 số 2, 3, 4, 5, 6, 7, 8, 9)
Vậy số các số tự nhiên chẵn có 3 chữ số là được lập từ các số trên là: 8.8.4 = 256 (số).
Câu 30:
Tính giá trị của biểu thức P = \(3C_n^3 + 2A_n^4 - 2n\). Biết giá trị của n thoả mãn \[A_n^2 - C_{n + 1}^{n - 1} = 4n + 6\] (n \( \in \)ℕ, n ≥ 2).
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có \[A_n^2 - C_{n + 1}^{n - 1} = 4n + 6\]
\[ \Leftrightarrow \frac{{n!}}{{\left( {n - 2} \right)!}} - \frac{{\left( {n + 1} \right)!}}{{2!\left( {n - 1} \right)!}} = 4n + 6\,\]
\( \Leftrightarrow \) 2(n – 1)n – n(n + 1) = 8n + 12
\( \Leftrightarrow \) n2 – 11n – 12 = 0 \( \Leftrightarrow \left[ \begin{array}{l}n = 12\\n = - 1\end{array} \right.\)
Kết hợp với điều kiện n = 12 thoả mãn điều kiện đề bài.
Vậy P = \(3C_n^3 + 2A_n^4 - 2n\) = \(3C_{12}^3 + 2A_{12}^4 - 2.12\) = 24396.
