10 câu hỏi trắc nghiệm thuộc Trắc nghiệm Ôn tập chương 1 có đáp án

Câu 1:

Cho tập hợp A = {1, 2, 3, 4, a, b}. Xét các mệnh đề sau đây:

(I): “3 ∈ A”.

(II): “{3, 4} ∈ A”.

(III): “{a, 3, b} ∈ A”.

Trong các mệnh đề sau, mệnh đề nào đúng

A. I đúng

B. I,II đúng

C. II, III đúng

D. I, III, đúng

Xem đáp án

Đáp án cần chọn là: A

3 là một phần tử của tập hợp A.

{3, 4} là một tập con của tập hợp A. Ký hiệu: {3, 4} ⊂ A.

{a, 3, b} là một tập con của tập hợp A. Ký hiệu: {a, 3, b} ⊂ A.

Câu 2:

Cho A = {0; 1; 2; 3; 4}, B = {2; 3; 4; 5; 6}. Tập hợp (A∖B) ∪ (B∖A) bằng?

A. {0; 1; 5; 6}

B. {1; 2}

C. {2; 3; 4}

D. {5; 6}

Xem đáp án

Đáp án cần chọn là: A

A = {0; 1; 2; 3; 4}, B = {2; 3; 4; 5; 6}.

A∖B = {0; 1}, B∖A = {5;6} ⇒ (A∖B) ∪ (B∖A) = {0; 1; 5; 6}

Câu 3:

Cho số tự nhiên n. Xét hai mệnh đề chứa biến: A(n):"n là số chẵn", B(n):"n² là số chẵn". Hãy phát biểu mệnh đề “∀n ∈ N, B(n) ⇒ A(n)”.

A. Với mọi số tự nhiên n, nếu n là số chẵn thì n²là số chẵn.

B. Tồn tại số tự nhiên n, nếu n² là số chẵn thì n là số chẵn

C. Với mọi số tự nhiên n, nếu n² là số chẵn thì n² là số chẵn

D. Với mọi số tự nhiên n, nếu n² là số chẵn thì n là số chẵn

Xem đáp án

Đáp án cần chọn là: D

“∀n ∈ N, B(n) ⇒ A(n)” : Với mọi số tự nhiên n, nếu n² là số chẵn thì n là số chẵn.

Câu 4:

Cho hai tập hợp A = {x ∈ R: x+2 ≥ 0}, B = {x ∈ R: 5−x ≥ 0}.

Khi đó A∖B là:

A. [−2; 5]

B. [−2; 6]

C. (5; +∞)

D. (2; +∞)

Xem đáp án

Đáp án cần chọn là: C

Ta có A = {x ∈ R: x + 2 ≥ 0} ⇒ A = [−2; +∞)

B = {x ∈ R: 5 − x ≥ 0} ⇒ B = (−∞; 5].

Vậy A∖B = (5; +∞).

Câu 5:

Cho tập hợp X = {1; 2; 3; 4}. Câu nào sau đây đúng?

A. Số tập con của X là 16

B. Số tập con của X gồm có 2 phần tử là 8

C. Số tập con của X chứa số 1 là 6

D. Số tập con của X gồm có 3 phần tử là

Xem đáp án

Đáp án cần chọn là: A

Số tập con của tập hợp X là: 2⁴=16 nên A đúng.

Các tập hợp con có 2 phần tử của X là:

{1;2},{1;3},{1;4},{2;3},{2;4},{3;4}

Có 6 tập hợp con gồm 2 phần tử nên B sai.

Số tập con của tập hợp X chứa số 1 là: 8 nên C sai.

Đó là các tập hợp: {1}, {1;2},{1;3}, {1;4}, {1;2;3}, {1;2;4}, {1;3;4}, {1;2;3;4}

Số tập con có 3 phần tử của tập hợp X là: 4, cụ thể:

{1;2;3},{1;2;4},{2;3;4},{1;3;4} nên D sai.

Câu 6:

Cho A = {x ∈ R ||mx−3| = mx−3}, B = {x ∈ R |x²−4 = 0}. Tìm m để B∖A=B

A. $- \frac{3}{2} \leq m \leq \frac{3}{2}$

B. $0 < m < \frac{3}{2}$ hoặc $- \frac{3}{2} < m < 0$

C. $- \frac{3}{2} < m < \frac{3}{2}$

D. $m \geq - \frac{3}{2}$

Xem đáp án

Đáp án cần chọn là: C

Ta có: $x \in A \Leftrightarrow m x - 3 \geq 0$

+ Nếu m = 0 thì $- 3 \geq 0$ (vô lí) nên $A = \emptyset$

+ Nếu m>0 thì $x \geq \frac{3}{m}$ hay $A = [\frac{3}{m}; + \infty)$

+ Nếu m<0 thì $x \leq \frac{3}{m}$ hay $A = (- \infty; \frac{3}{m}]$

$x \in B \Leftrightarrow [\begin{matrix} x = 2 \\ x = - 2 \end{matrix}$ hay $B = \{- 2; 2\}$

Ta có:B \ $A = B \Leftrightarrow B \cap A = \emptyset \Leftrightarrow [\begin{matrix} m = 0 \\ \{\begin{matrix} m > 0 \\ \frac{3}{m} > 2 \end{matrix} \\ \{\begin{matrix} m < 0 \\ \frac{3}{m} < - 2 \end{matrix} \end{matrix} \Leftrightarrow [\begin{matrix} m = 0 \\ 0 < m < \frac{3}{2} \\ - \frac{3}{2} < m < 0 \end{matrix}$ $\Leftrightarrow - \frac{3}{2} < m < \frac{3}{2}$

Câu 7:

Phát biểu mệnh đề P ⇒ Q và phát biểu mệnh đề đảo, xét tính đúng sai của các mệnh đề đó với: P: ″2 > 9″ và Q: ″4 < 3″. Chọn đáp án đúng:

A. Mệnh đề P ⇒ Q là " Nếu 2 > 9 thì 4 < 3", mệnh đề này đúng vì mệnh đề P sai. Mệnh đề đảo là Q ⇒ P: " Nếu 4 < 3 thì 2 > 9", mệnh đề này đúng vì mệnh đề Q đúng.

B. Mệnh đề P ⇒ Q là " Nếu 2 > 9 thì 4 < 3", mệnh đề này sai vì mệnh đề P sai. Mệnh đề đảo là Q ⇒ P: " Nếu 4 < 3 thì 2 > 9", mệnh đề này đúng vì mệnh đề Q sai

C. Mệnh đề P ⇒ Q là " Nếu 2 > 9 thì 4 < 3", mệnh đề này sai vì mệnh đề P sai. Mệnh đề đảo là Q ⇒ P: " Nếu 4 < 3 thì 2 > 9", mệnh đề này sai vì mệnh đề Q sai

D. Mệnh đề P ⇒ Q là " Nếu 2 > 9 thì 4 < 3", mệnh đề này đúng vì mệnh đề P sai. Mệnh đề đảo là Q ⇒ P: " Nếu 4 < 3 thì 2 > 9", mệnh đề này đúng vì mệnh đề Q sai.

Xem đáp án

Đáp án cần chọn là: D

Mệnh đề P ⇒ Q là " Nếu 2 > 9 thì 4 < 3", mệnh đề này đúng vì mệnh đề 2 > 9 sai.

Mệnh đề đảo là Q ⇒ P: " Nếu 4 < 3 thì 2 > 9", mệnh đề này đúng vì mệnh đề 4<3 sai.

Câu 8:

Cho các tập hợp khác rỗng A = (−∞; m) và B = [2m−2; 2m+2]. Tìm m ∈ R để (C_RA) ∩ B ≠ ∅.

A. m ≥ 2

B. m < −2

C. m ≥ −2

D. m < 2

Xem đáp án

Đáp án cần chọn là: C

Ta có: C_RA = [m; +∞)

Để C_RA ∩ B ≠ ∅ ⇔ 2m+2 ≥ m ⇔ m ≥ −2

Câu 9:

Cho hai tập hợp A = [1; 3] và B = [m; m+1]. Tìm tất cả giá trị của tham số m để B⊂A.

A. m=1

B. 1<m<2

C. 1≤m≤2

D. m=2

Xem đáp án

Đáp án cần chọn là: C

Ta có: $B \subset A \Leftrightarrow 1 \leq m \leq m + 1 \leq 3 \Leftrightarrow \{\begin{matrix} m \geq 1 \\ m + 1 \leq 3 \end{matrix} \Leftrightarrow \{\begin{matrix} m \geq 1 \\ m \leq 2 \end{matrix}$

Vậy $1 \leq m \leq 2$

Câu 10:

Lớp 10A có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hoá, 3 học sinh giỏi cả Toán và Lý, 4 học sinh giỏi cả Toán và Hoá, 2 học sinh giỏi cả Lý và Hoá, 1 học sinh giỏi cả ba môn Toán, Lý, Hoá. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hoá) của lớp 10A là:

A. 9

B. 18

C. 10

D. 28

Xem đáp án

Đáp án cần chọn là: C

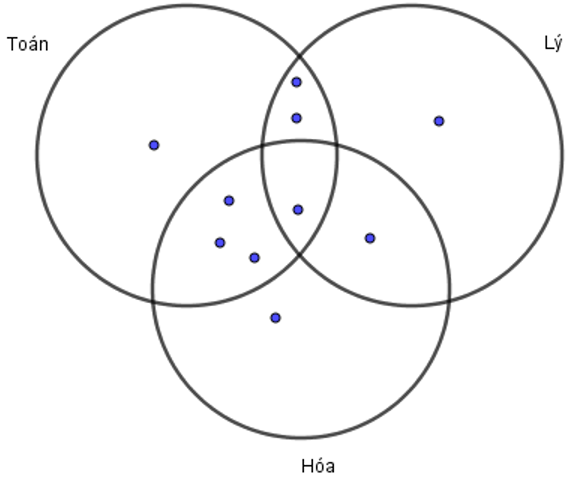
Số học sinh giỏi toán, lý mà không giỏi hóa: 3−1=2.

Số học sinh giỏi toán, hóa mà không giỏi lý: 4−1=3.

Số học sinh giỏi hóa, lý mà không giỏi toán: 2−1=1.

Số học sinh chỉ giỏi môn lý: 5−2−1−1=1.

Số học sinh chỉ giỏi môn hóa: 6−3−1−1=1.

Số học sinh chỉ giỏi môn toán: 7−3−2−1=1.

Số học sinh giỏi ít nhất một (môn toán, lý, hóa) là số học sinh giỏi 1 môn hoặc 2 môn hoặc cả 3 môn: 1 + 1 + 1 + 1 + 2 + 3 + 1 = 10.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Ôn tâp chương 1 có đáp án

Trắc nghiệm Ôn tập chương 1 có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương