Phương trình lôgarit và cách giải các dạng bài tập - Toán lớp 12
Hamchoi.vn giới thiệu 50 Phương trình lôgarit và cách giải các dạng bài tập - Toán lớp 12 lớp 12 gồm các dạng bài tập có phương pháp giải chi tiết và các bài tập điển hình từ cơ bản đến nâng cao giúp học sinh biết cách làm. Bên cạnh có là 25 bài tập vận dụng để học sinh ôn luyện dạng Toán 12 này.
Phương trình lôgarit và cách giải các dạng bài tập - Toán lớp 12
I. LÝ THUYẾT
a. Phương trình lôgarit cơ bản:
Phương trình lôgarit cơ bản có dạng: ,
Theo định nghĩa logarit ta có
b. Phương pháp giải phương trình lôgarit
Biến đổi, quy về cùng cơ số:
Đặt ẩn phụ:
Mũ hóa hai vế:
Giải bằng phương pháp đồ thị:
Giải phương trình:
Xem phương trình là phương trình hoành độ giao điểm của hai đồ thị và . Khi đó ta thực hiện hai bước:
Bước 1. Vẽ đồ thị các hàm số và .
Bước 2. Kết luận nghiệm của phương trình đã cho là số giao điểm của hai đồ thị.
Sử dụng tính đơn điệu của hàm số:
Sử dụng đánh giá
II. CÁC DẠNG BÀI VÀ PHƯƠNG PHÁP GIẢI
Dạng 1. Phương trình loogarit cơ bản
A. Phương pháp giải
Xét phương trình lôgarit cơ bản:,
Bước 1: Nêu điều kiện để f(x) có nghĩa
Bước 2: Giải phương trình
Bước 3: Kết luận nghiệm của phương trình.
B. Ví dụ minh họa
Câu 1: Tìm tập nghiệm của phương trình .
A.
B. .
C.
D. .
Hướng dẫn giải
Chọn B.
Ta có
Vậy tập nghiệm của phương trình S = {18}.
Câu 2: Số nghiệm của phương trình .
A. 2.
B. 1
C. 0
D. một số khác.
Hướng dẫn giải
Chọn A.
Điều kiện
Ta có
(thỏa mãn).
Vậy phương trình có hai nghiệm.
Câu 3: Số nghiệm của phương trình là
A. 1
B. 3
C. 2
D. 0
Hướng dẫn giải
Chọn C.
Điều kiện xác định:
hoặc (thỏa mãn).
Vậy phương trình có hai nghiệm.
Câu 4: Gọi là 2 nghiệm của phương trình . Khi đó bằng:
A. -3
B. -2
C.
D.
Hướng dẫn giải
Chọn A.
[Phương pháp tự luận]
Điều kiện:
(thỏa mãn)
Vậy
[Phương pháp trắc nghiệm]
Dùng chức năng SOLVE trên máy tính bỏ túi tìm được 2 nghiệm và lưu 2 nghiệm vào A và B. Tính A + B = – 3.
Câu 5: Gọi là nghiệm của phương trình . Khi đó tích bằng:
A. -2
B. 1.
C. -1
D. 2.
Hướng dẫn giải
Chọn A.
Điều kiện hoặc
Dạng 2. Phương pháp đưa về cùng cơ số
A. Phương pháp giải
Xét phương trình cùng cơ số:
Bước 1: Nêu điều kiện
Bước 2 Giải phương trình:
Bước 3: So sánh với điều kiện và kết luận.
B. Ví dụ minh họa
Câu 1: Tập nghiệm của phương trình là
A.
B. {2; 41}
C.
D.
Hướng dẫn giải.
Chọn A.
Điều kiện:
Khi đó PT
Đối chiếu điều kiện ta được tập nghiệm của phương trình là .
Câu 2: Cho phương trình . Mệnh đề nào dưới đây đúng?
A.
B.
C.
D.
Hướng dẫn giải
Chọn A.
Điều kiện của phương trình là
Khi đó
Vậy phương trình đã cho tương đương với
Câu 3: Số nghiệm của phương trình là:
A. 0.
B. 2.
C. 3.
D. 1.
Hướng dẫn giải
Chọn D.
[Phương pháp tự luận]
Điều kiện
Khi đó, ta có:
Kết hợp với điều kiện, x = 5 là giá trị cần tìm.
[Phương pháp trắc nghiệm]
Nhập vào màn hình máy tính
Ấn SHIFT CALC nhập X = 4 (chọn X thỏa điều kiện xác định của phương trình), ấn =. Máy hiện X = 5.
Ấn Alpha X Shift STO A
Ấn AC. Viết lại phương trình:
Ấn SHIFT CALC. Máy hỏi A? ẤN = Máy hỏi X? Ấn 7 =.
Máy không giải ra nghiệm. Vậy đã hết nghiệm.
Câu 4: Phương trình có tập nghiệm là tập nào sau đây?
A.
B.
C.
D.
Hướng dẫn giải.
Chọn D.
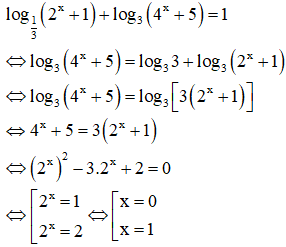
Câu 5: Tìm tất cả các giá trị thực của tham số m để phương trình có nghiệm?
A.
B.
C.
D.
Hướng dẫn giải
Chọn A.
[Phương pháp tự luận]
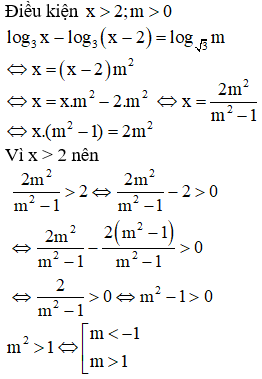
Kết hợp với điều kiện m > 0, ta được m > 1.
Phương trình có nghiệm x >2 khi m >1 ,chọn đáp án A
[Phương pháp trắc nghiệm]
Thay m =0 (thuộc C, D) vào biểu thức không xác định, vậy loại C, D,
Thay m =1 (thuộc B) ta được phương trình tương đương vô nghiệm
Vậy chọn đáp án A.
Dạng 3. Phương pháp đặt ẩn phụ
A. Phương pháp giải
Xét phương trình:
Bước 1: Đặt điều kiện: g(x) > 0
Bước 2: Đặt
Giải phương trình f(t) = 0, tìm t.
Bước 3: Thay vào phương trình: , tìm x.
Bước 4: Kết hợp với điều kiện và kết luận.
B. Ví dụ minh họa
Câu 1: Nếu đặt thì phương trình trở thành phương trình nào?
A.
B.
C.
D.
Hướng dẫn giải
Chọn A
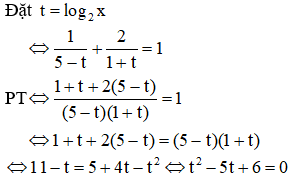
Câu 2: Gọi là 2 nghiệm của phương trình . Khi đó bằng:
A.
B.
C.
D.
Hướng dẫn giải
Chọn B.
[Phương pháp tự luận]
Điều kiện:
Đặt ,điều kiện . Khi đó phương trình trở thành:
Vậy
[Phương pháp trắc nghiệm]
Dùng chức năng SOLVE trên máy tính bỏ túi tìm được 2 nghiệm là và .
Câu 3: Phương trình có tập nghiệm là:
A.
B.
C.
D.
Hướng dẫn giải
Chọn C.
[Phương pháp tự luận]
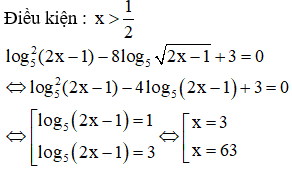
[Phương pháp trắc nghiệm]
Thay x =1 (thuộc B, D) vào vế trái ta được 3=0 vô lý, vậy loại B, D,
Thay x = - 1 vào ta được không xác định, nên loại A
Vậy chọn đáp án C.
Câu 4: Gọi , là các nghiệm của phương trình . Giá trị của biểu thức bằng bao nhiêu?
A. 20
B. 5
C. 36
D. 25
Hướng dẫn giải.
Chọn A.
Điều kiện x >0. Giải phương trình bậc hai với ẩn là ta được:
Khi đó, .
Câu 5:Tìm tất cả các giá trị của tham số m để phương trình có nghiệm x >2
A.
B.
C.
D.
Hướng dẫn giải
Chọn D.
(1).
Đặt , phương trình (1) trở thành: (2).
Phương trình (1) có nghiệm phương trình (2) có nghiệm:
Xét hàm số ( loại).
Bảng biến thiên
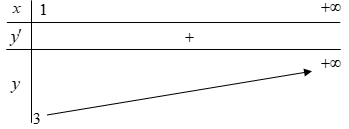
Từ Bảng biến thiên suy ra phương trình (2) có nghiệm
Dạng 4. Phương pháp mũ hóa
A. Phương pháp giải
Xét phương trình:
Bước 1: Đặt điều kiện g(x) > 0
Bước 2: Giải phương trình:
Bước 3: Kết hợp với điều kiện, kết luận nghiệm.
Câu 1: Cho x thỏa mãn phương trình . Giá trị của biểu thức là
A.
B.
C.
D.
Hướng dẫn giải
Chọn C.
Ta có
Vậy
Câu 2: Phương trình có bao nhiêu nghiệm?
A. 1.
B. 2.
C. 3.
D. 0.
Hướng dẫn giải
Chọn B.
[Phương pháp tự luận]
Điều kiện
(thỏa mãn).
Vậy phương trình đã cho có 2 nghiệm.
[Phương pháp trắc nghiệm]
Nhập vào màn hình máy tính:
Ấn SHIFT CALC nhập X=5, ấn =. Máy hiện X=0.
Ấn Alpha X Shift STO A
Ấn AC. Viết lại phương trình:
Ấn SHIFT CALC. Máy hỏi A? ẤN = Máy hỏi X? Ấn 5 =. Máy hiện X=-1.
Ấn Alpha X Shift STO B.
Ấn AC. Viết lại phương trình:
Ấn SHIFT CALC. Máy hỏi A? ẤN = Máy hỏi B? Ấn =. Máy hỏi X? Ấn 1=
Máy không giải ra nghiệm. Vậy đã hết nghiệm.
Câu 3: Số nghiệm nguyên dương của phương trình là:
A. 2.
B. 1.
C. 3.
D. 0.
Hướng dẫn giải
Chọn B.
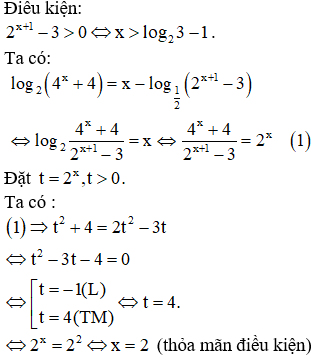
Vậy nghiệm của phương trình đã cho là x =2.
Câu 4: Tìm tất cả các giá trị của m để phương trình có nghiệm duy nhất.
A.
B.
C.
D.
Hướng dẫn giải.
Chọn C.
Điều kiện
PT:
Xét trên ta có bảng biến thiên:
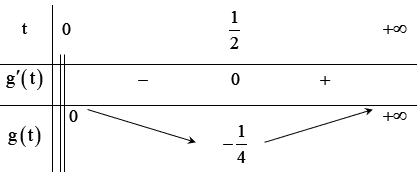
PT đã cho có nghiệm duy nhất:
.
Dạng 5. Phương pháp hàm số, đồ thị và đánh giá
A. Phương pháp giải
Giải bằng phương pháp đồ thị:
Giải phương trình:
Xem phương trình là phương trình hoành độ giao điểm của hai đồ thị và . Khi đó ta thực hiện hai bước:
Bước 1. Vẽ đồ thị các hàm số và .
Bước 2. Kết luận nghiệm của phương trình đã cho là số giao điểm của hai đồ thị.
Sử dụng tính đơn điệu của hàm số:
Sử dụng đánh giá
B. Ví dụ minh họa
Câu 1: Phương trình: có tổng bình phương các nghiệm bằng:
A. 5
B. 1
C. 9
D. 25
Hướng dẫn giải
Chọn B.
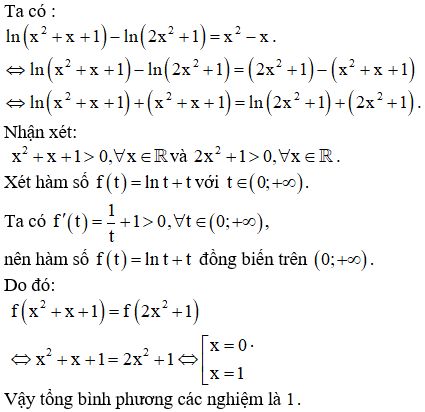
Câu 2: Tìm tất cả các giá trị của m để phương trình có ba nghiệm phân biệt.
A.
B.
C.
D.
Hướng dẫn gải:
Chọn B.
Điều kiện:
Phương trình đã cho tương đương với:
Phương trình là phương trình hoành độ giao điểm của đồ thị hàm số và đường thẳng (cùng phương với trục hoành).
Xét hàm số xác định trên .
Ta có :
Đồ thị
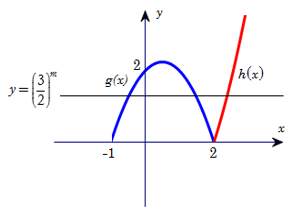
Dựa vào đồ thị, ta thấy để phương trình có ba nghiệm phân biệt khi
Chọn B.
Câu 3: Cho phương trình có tổng tất cả các nghiệm bằng
A. 5
B. 3
C.
D. 2
Hướng dẫn giải
Chọn B.

III. BÀI TẬP TỰ LUYỆN
Câu 1: Tìm nghiệm của phương trình
A.
B.
C.
D.
Câu 2: Phương trình có tất cả bao nhiêu nghiệm thực?
A. 2
B. 3
C. 4
D. 8
Câu 3: Số nghiệm của phương trình là:
A. 2.
B. 0.
C. 1.
D. 3.
Câu 4: Tìm tập nghiệm S của phương trình
A.
B.
C.
D.
Câu 5: Số nghiệm của phương trình là:
A. 3.
B. 4.
C. 1.
D. 2.
Câu 6: Gọi là 2 nghiệm của phương trình .
Khi đó bằng:
A. 5.
B. 3.
C. -2
D. 7.
Câu 7: Số nghiệm của phương trình là:
A. 0.
B. 2.
C. 3.
D. 1.
Câu 8: Giải phương trình
A.
B.
C.
D.
Câu 9: Phương trình có 2 nghiệm trong đó .Giá trị của là
A. 5.
B. 14.
C. 3.
D. 13.
Vậy .
Câu 10: Số nghiệm của phương trình là:
A. 0.
B. 2.
C. 3.
D. 1.
Câu 11: Với giá trị m bằng bao nhiêu thì phương trình có nghiệm bằng 1?
A.
B.
C. m <3
D. m >3
Câu 12: Phương trình có bao nhiêu nghiệm trên R?
A. 0
B. 1
C. 2
D. 3
Câu 13: Tìm tất cả các giá trị của m để phương trình có ba nghiệm phân biệt.
A. m >3
B. m <2
C. m >0
D. m =2
Câu 14: Nếu đặt thì phương trình trở thành phương trình nào?
A.
B.
C.
D.
Câu 15: Phương trình có tích các nghiệm là:
A.
B.
C. e
D. 2
Câu 16: Nghiệm lớn nhất của phương trình là :
A. 100.
B. 2.
C. 10.
D. 1000.
Câu 17: Nếu đặt thì phương trình trở thành phương trình nào?
A.
B.
C.
D.
Câu18: Nghiệm nguyên của phương trình là:
A. x =1
B. x =-1
C. x =2
D. x =3
Câu19: Điều kiện cần và đủ của tham số m để phương trình có hai nghiệm phân biệt thuộc là
A.
B.
C.
D. .
Câu 20. Cho phương trình . Gọi lần lượt là 2 nghiệm của phương trình. Khi đó tích ab bằng:
A. 0
B. 1
C. .
D.
Câu 21: Với giá trị nào của m thì phương trình có 2 nghiệm phân biệt?
A.
B.
C.
D.
Câu 22: Phương trình có bao nhiêu nghiệm
A. 1 nghiệm
B. 2 nghiệm
C. 3 nghiệm
D. Vô nghiệm
Câu 23: Số nghiệm của phương trình là
A. 3
B. 2
C. 1
D. 4
Câu 24: Tập hợp các giá trị của m để phương trình có nghiệm thuộc là
A.
B.
C.
D.
Câu 25: Biết phương trình có nghiệm duy nhất trong đó a,b là các số nguyên. Tính a +b?
A. 5
B. -1
C. 1
D. 2
Đáp án

Các dạng bài tập Hàm số lũy thừa, Hàm số mũ và hàm số logarit
Bài viết liên quan
- Hàm số lũy thừa, hàm số mũ, hàm số logarit và cách giải bài tập - Toán lớp 12
- Phương trình mũ và cách giải các dạng bài tập - Toán lớp 12
- Bất phương trình mũ và cách giải các dạng bài tập - Toán lớp 12
- Bất phương trình logarit và cách giải các dạng bài tập - Toán lớp 12
- Các dạng toán về lãi suất ngân hàng và cách giải - Toán lớp 12
