Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) - đề 5
-
4690 lượt thi
-
5 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Điểm kiểm tra 1 tiết đại số của học sinh lớp 7A được ghi lại như sau: 6 4 9 7 8 8 4 8 8 10
10 9 8 7 7 6 6 8 5 6
4 9 7 6 6 7 4 10 9 8 a) Lập bảng tần số;
b) Tính số trung bình cộng và tìm mốt của dấu hiệu
Xem đáp án
a) Lập bảng tần số: (1 điểm)
|
Giá trị (x) |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
Tần số (n) |
4 |
1 |
6 |
5 |
7 |
4 |
3 |
N = 30 |
b) Số trung bình cộng của dấu hiệu là:
Mốt của dấu hiệu là: . (0,5 điểm)
Câu 2:
a) Thu gọn và xác định hệ số, phần biến, bậc của đơn thức P;
b) Tính giá trị của P tại x = –1 và y = 2.
Xem đáp án
a)
Hệ số: 3
Phần biến: x3y2
Bậc của đơn thức: 5b) Thay x = –1 và y = 2 vào đơn thức P
P = 3.( –1)3.22 = –12
Vậy P = –12 tại x = –1 và y = 2. (0,5 điểm)
Câu 3:
Cho 2 đa thức sau:
A(x) = 4x3 – 7x2 + 3x – 12
B(x) = – 2x3 + 2x2 + 12 + 5x2 – 9x
a) Thu gọn và sắp xếp đa thức B(x) theo lũy thừa giảm dần của biến;
b) Tính A(x) + B(x) và B(x) – A(x).
Xem đáp án
a) B(x) = –2x3 + 2x2 + 12 + 5x2 – 9x
= –2x3 + (2x2 + 5x2) + 12 – 9x
= –2x3 + 7x2 + 12 – 9x
Sắp xếp: B(x) = –2x3 + 7x2 – 9x + 12A(x) = 4x3 – 7x2 + 3x – 12
B(x) = –2x3 + 7x2 – 9x + 12
A(x) + B(x) = 2x3 – 6x
Nên A(x) + B(x) = 2x3 – 6x (0,5 điểm)
|
– |
A(x) = 4x3 – 7x2 + 3x – 12
B(x) – A(x) = –6x3 + 14x2 –12x + 24
Suy ra B(x) – A(x) = –6x3 + 14x2 –12x + 24Câu 4:
a) M(x) = 2x – 6;
b) N(x) = x2 + 2x + 2015.
Xem đáp án
a) M(x) = 2x – 6
Ta có: M(x) = 0 hay 2x – 6 =0
2x = 6
x = 3
Vậy nghiệm của đa thức M(x) là x = 3. (1 điểm)
b) N(x) = x2 + 2x + 2015
Ta có: x2 + 2x + 2015 = x2 + x + x + 1 + 2014
= x(x + 1) + (x + 1) + 2014
= (x + 1)(x + 1) + 2014
= (x + 1)2 + 2014
Vì (x + 1)2 0 với mọi x
(x + 1)2 + 2014 2014 > 0 với mọi x
N(x) > 0 với mọi x
Vậy đa thức N(x) không có nghiệm. (0,5 điểm)
Câu 5:
Cho ∆ABC vuông tại A, vẽ trung tuyến AM (M Î BC). Từ M kẻ MH
AC (H 
AC), trên tia đối của tia MH lấy điểm K sao cho MK = MH.
a) Chứng minh ∆MHC = ∆MKB;
b) Chứng minh AB // MH;
c) Gọi G là giao điểm của BH và AM, I là trung điểm của AB. Chứng minh I, G, C thẳng hàng.
Xem đáp án
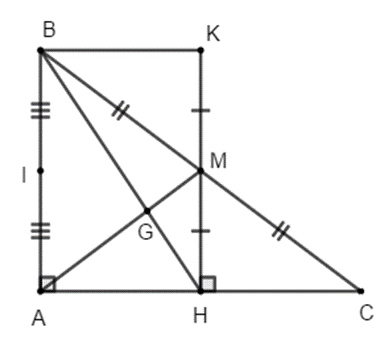
a) Xét ∆MHC và ∆MKB có
MH = MK (gt)
(hai góc đối đỉnh)
MC = MB (M là trung điểm của BC)
Do đó: ∆MHC = ∆MKB (c.g.c) (1 điểm)
b) Ta có MH AC (gt)
AB AC (∆ABC vuông tại A)
Nên AB // MH. (1 điểm)
c) Xét ∆ABH vuông tại A và ∆KHB vuông tại H có:
BH: cạnh huyền chung
(AB // MH)
Do đó: ∆ABH = ∆KHB (ch-gn)
AH = BK (hai cạnh tương ứng)
Mà BK = HC (∆MHC = ∆MKB)
Nên AH = HC H là trung điểm của AC
Do đó G là giao điểm của hai trung tuyến BH và AM trong tam giác ABC
G là trọng tâm của tam giác ABC
Mà CI là trung tuyến của tam giác ABC (do I là trung điểm của AB)
Vậy G thuộc trung tuyến CI hay I, G, C thẳng hàng. (1 điểm)