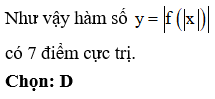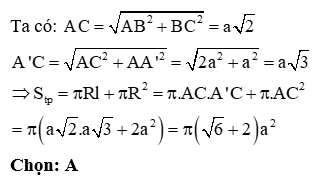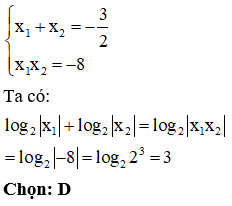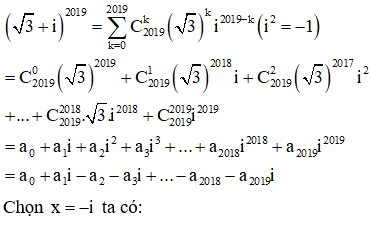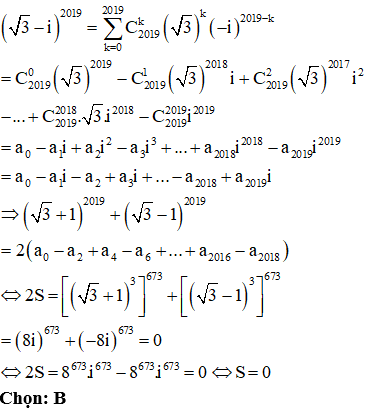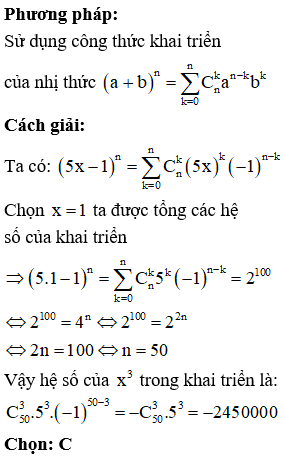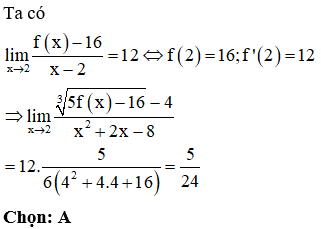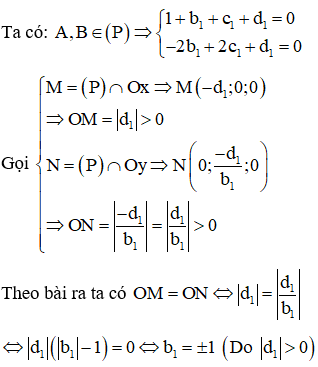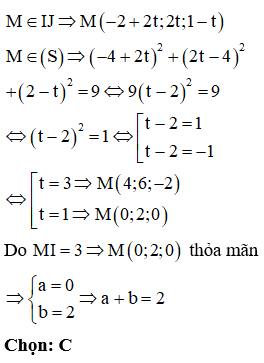50 câu hỏi trắc nghiệm thuộc Tổng hợp 20 đề thi thử thpt quốc gia môn Toán cực hay có lời giải chi tiết abc - đề 14

Câu 1:

Trong các mệnh đề sau, mệnh đề nào sai?

A. $\lim_{x \to - \infty} (\sqrt{x^{2} - x + 1} + x - 2) = - \frac{3}{2}$

B. $\lim_{x \to {(- 1)}^{-}} \frac{3 x - 2}{x + 1} = - \infty$

C. $\lim_{x \to + \infty} (\sqrt{x^{2} - x + 1} + x - 2) = + \infty$

D. $\lim_{x \to {(- 1)}^{+}} \frac{3 x - 2}{x + 1} = - \infty$

Xem đáp án

Phương pháp:

Sử dụng các phương pháp tính giới hạn hàm số để tính các giới hạn và chọn đáp án đúng.

Cách giải:

Ta có:

Câu 2:

Tập nghiệm của bất phương trình $\frac{\log (x^{2} - 9)}{\log (3 - x)} \leq 1$ là:

A. $\emptyset$

B. $(- 4; - 3)$

C. $(3; 4]$

D. $[- 4; - 3)$

Xem đáp án

Chọn: D

Câu 3:

Cho số phức $z \neq 0$ . Khẳng định nào sau đây sai?

A. $z + \bar{z}$ là số thực

B. $z - \bar{z}$ là số ảo

C. $\frac{z}{\bar{z}}$ là số thuần ảo

D. $z . \bar{z}$ là số thực

Xem đáp án

Câu 4:

Vecto nào sau đây là một vecto chỉ phương của đường thẳng $\frac{x + 2}{3} = \frac{y + 1}{- 2} = \frac{z - 3}{- 1}$ ?

A. (-3;2;1)

B. (-2;1;-3)

C. (3;-2;1)

D. (2;1;3)

Xem đáp án

Câu 5:

Trong không gian với hệ tọa độ Oxyz cho ba điểm $A (0; 2; - 1), B (- 5; 4; 2) v à C (- 1; 0; 5)$ . Tọa độ trọng tâm tam giác ABC là:

A. (-1;1;1)

B. (-2;2;2)

C. (-6;6;6)

D. (-3;3;3)

Xem đáp án

Câu 6:

Số giao điểm của đồ thị hàm số $y = x^{2} |x^{2} - 4|$ với đường thẳng y = 3 là:

A. 8

B. 2

C. 4

D. 6

Xem đáp án

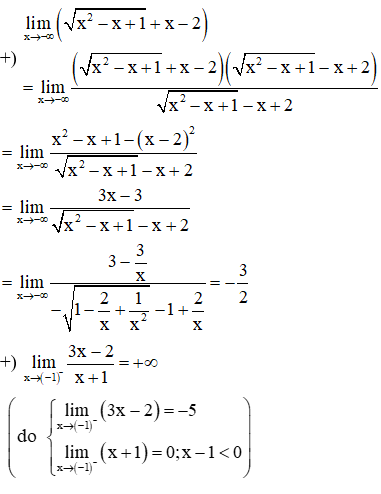
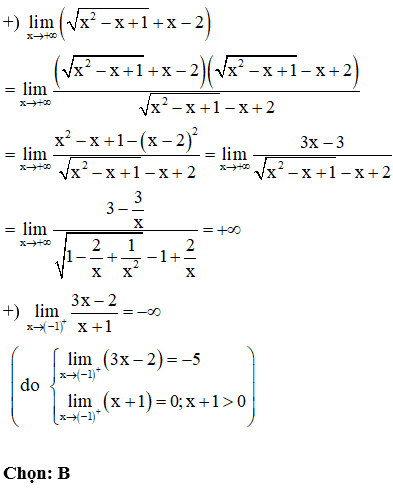
Câu 7:

Trong không gian với hệ tọa độ Oxyz phương trình nào sau đây không phải là phương trình của một mặt cầu?

A. $x^{2} + y^{2} + z^{2} + x - 2 y + 4 z - 3 = 0$

B. $2 x^{2} + 2 y^{2} + 2 z^{2} - x - y - z = 0$

C. $x^{2} + y^{2} + z^{2} - 2 x + 4 y - 4 z + 10 = 0$

D. $2 x^{2} + 2 y^{2} + 2 z^{2} + 4 x + 8 y + 6 z + 3 = 0$

Xem đáp án

=> phương trình này không phải là phương trình mặt cầu.

Chọn: C

Câu 8:

Cho một cấp số cộng $(u_{n}) c ó u_{1} = 5$ và tổng 40 số hạng đầu bằng 3320. Tìm công sai của cấp số cộng đó.

A. 4

B. -4

C. 8

D. -8

Xem đáp án

Câu 9:

Đồ thị hàm số $y = \frac{x - 1}{\sqrt{25 - x^{2}}}$ có bao nhiêu đường tiệm cận?

A. 1

B. 2

C. 3

D. .4

Xem đáp án

Câu 10:

Trong không gian với hệ tọa độ cho điểm $A (- 3; 1; 2)$ . Tọa độ điểm A' đối xứng với điểm A qua trục Oy là:

A. (3;-1;-2)

B. (3;-1;2)

C. (-3;-1;2)

D. (3;1;-2)

Xem đáp án

Câu 11:

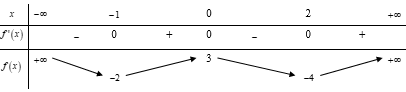
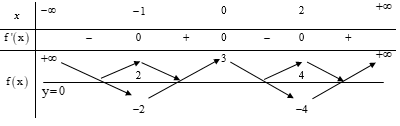
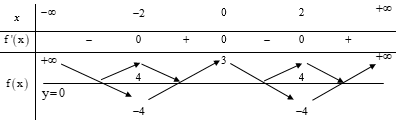
Tập giá trị của hàm số $y = \sqrt{x - 3} + \sqrt{7 - x}$ là:

A. $[2; 2 \sqrt{2}]$

B. [3;7]

C. $[0; 2 \sqrt{2}]$

D. (3;7)

Xem đáp án

Phương pháp:

Tìm TXĐ của hàm số sau đó xét sự biến thiên, lập BBT và tìm tập giá trị của hàm số.

Cách giải:

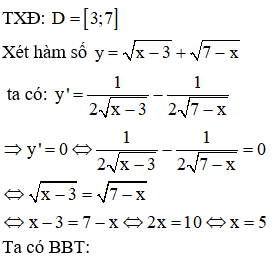
Câu 12:

Đạo hàm của hàm số $f (x) = \sqrt{\ln (\ln x)}$ là:

A. $f' (x) = \frac{1}{2 x \ln x \sqrt{\ln (\ln x)}}$

B. $f' (x) = \frac{1}{x \ln x \sqrt{\ln (\ln x)}}$

C. $f' (x) = \frac{1}{2 x \sqrt{\ln (\ln x)}}$

D. $f' (x) = \frac{1}{\ln x \sqrt{\ln (\ln x)}}$

Xem đáp án

Phương pháp:

Sử dụng công thức đạo hàm của các hàm số cơ bản và hàm hợp:

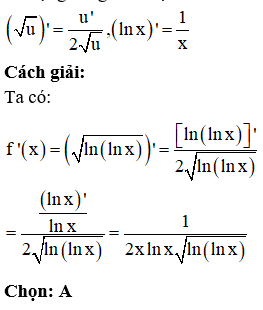
Câu 13:

Tính diện tích hình phẳng giới hạn bởi các điểm biểu diễn các số phức thỏa mãn $|z + 2 - i| + |z - 4 - i| = 10$

A. $12 π$

B. $20 π$

C. $15 π$

D. Đáp án khác

Xem đáp án

Phương pháp:

Tìm tập hợp các điểm biểu diễn số phức bài cho sau đó tính diện tích hình phẳng được giới hạn bởi các điểm đó.

Cách giải:

Câu 14:

Cho hàm số f(x) với bảng biến thiên dưới đây:

Hỏi hàm số $y = |f (|x|)|$ có bao nhiêu cực trị?

A. 5

B. 3

C. 1

D. 7

Xem đáp án

Câu 15:

Cho lăng trụ $A B C . A' B' C'$ . Gọi M, N lần lượt là trung điểm của AA' và BC' . Khi đó đường thẳng AB' song song với mặt phẳng:

A. (C'MN)

B. (A'CN)

C. (A'BN)

D. (BMN)

Xem đáp án

Phương pháp:

Sử dụng quan hệ song song trong không gian để chứng minh và chọn đáp án đúng.

Cách giải:

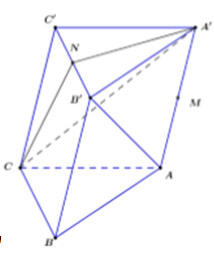
Câu 16:

Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \frac{x + m}{x + 1}$ trên đoạn [1;2] bằng 8 (m là tham số thực). Khẳng định nào sau đây là đúng?

A. 0 < m < 4

B. 4 < m < 8

C. 8 < m < 10

D. m > 10

Xem đáp án

Vì hàm số đã cho là hàm bậc nhất trên bậc nhất nên hàm số đơn điệu trên từng khoảng xác định của hàm số.

Câu 17:

Số $20182019^{20192020}$ có bao nhiêu chữ số?

A. 147501991

B. 147501992

C. 147433277

D. 147433276

Xem đáp án

Câu 18:

Phương trình $\cos 2 x + 2 \cos x - 3 = 0$ có bao nhiêu nghiệm trong khoảng $(0; 2019)$ ?

A. 1009

B. 1010

C. 320

D. 321

Xem đáp án

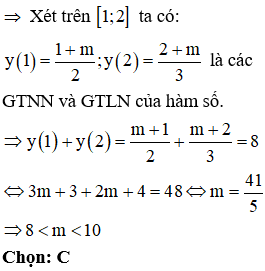
Câu 19:

Cho hàm số $f (x) = \{\begin{cases} 7 - 4 x^{2} k h i 0 \leq x \leq 1 \\ 4 - x^{2} k h i x > 1 \end{cases}$ . Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $f (x)$ và các đường thẳng $x = 0, x = 3, y = 0$

A. $\frac{16}{3}$

B. $\frac{20}{3}$

C. 10

D. 9

Xem đáp án

Phương pháp:

Công thức tính diện tích hình phẳng được giới hạn bởi các đường thẳng

Câu 20:

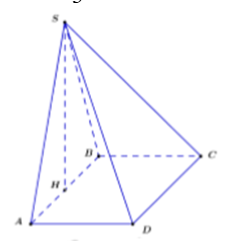
Cho hình chóp tứ giác SABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là một tam giác đều và nằm trong một mặt phẳng vuông góc với đáy (ABCD). Tính thể tích khối chóp SABCD.

A. $\frac{a^{3}}{6}$

B. $\frac{a^{3} \sqrt{3}}{2}$

C. $\frac{a^{3} \sqrt{3}}{6}$

D. $\frac{a^{3}}{2}$

Xem đáp án

Phương pháp:

Công thức tính thể tích khối chóp có diện tích đáy S và chiều cao h là: $V = \frac{1}{3} S h$

Cách giải:

Câu 21:

Cho số tự nhiên n thỏa mãn $C_{n}^{2} + A_{n}^{2} = 15 n$ . Mệnh đề nào sau đây là đúng?

A. n chia hết cho 7

B. n không chia hết cho 2

C. n chia hết cho 5

D. n không chia hết cho 11

Xem đáp án

Câu 22:

Trong không gian với hệ tọa độ Oxyz, cho điểm $H (1; 2; - 2)$ . Mặt phẳng $(α)$ đi qua H và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C sao cho H là trực tâm của $Δ A B C$ . Tính diện tích mặt cầu ngoại tiếp tứ diện OABC.

A. $\frac{81 π}{2}$

B. $\frac{243 π}{2}$

C. $81 π$

D. $243 π$

Xem đáp án

Phương pháp:

Gọi tọa độ các điểm A, B, C.

Lập phương trình mặt phẳng đi qua H và cắt các trục Ox, Oy, Oz bằng phương trình đoạn chắn.

Từ đó tìm được các điểm A, B, C. Từ đó tính được bán kính mặt cầu ngoại tiếp tứ diện OABC.

Câu 23:

Cho hình lập phương $A B C D . A' B' C' D'$ cạnh a. Tính diện tích toàn phần của vật tròn xoay thu được khi quay tam giác $A A' C'$ quanh trục AA'

A. $π (\sqrt{6} + 2) a^{2}$

B. $π (\sqrt{3} + 2) a^{2}$

C. $2 π (\sqrt{2} + 1) a^{2}$

D. $2 π (\sqrt{6} + 1) a^{2}$

Xem đáp án

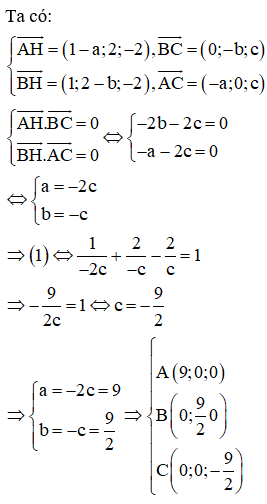
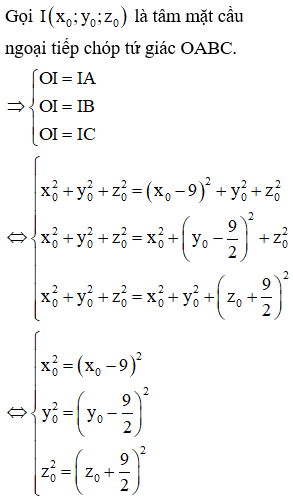
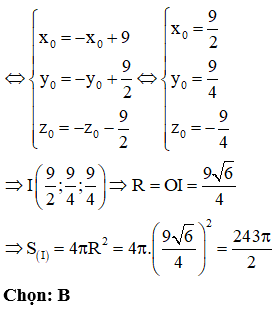
Câu 24:

Một mô hình gồm các khối cầu xếp chồng lên nhau tạo thành một cột thẳng đứng. Biết rằng mỗi khối cầu có bán kính gấp đôi bán kính của khối cầu nằm ngay trên nó và bán kính khối cầu dưới cùng là 50cm. Hỏi mệnh đề nào sau đây là đúng?

A. Mô hình có thể đạt được chiều cao tùy ý.

B. Chiều cao mô hình không quá 1,5 mét.

C. Chiều cao mô hình tối đa là 2 mét.

D. Chiều cao mô hình dưới 2 mét.

Xem đáp án

Phương pháp:

Gọi các quả cầu được xếp trong mô hình là n quả.

Bán kính các quả cầu tạo thành cấp số nhân có công bội là 2.

Tổng của n số hạng đầu của CSN có số hạng đầu là $u_{1}$ và công bội q:

Câu 25:

Cho khối chóp tứ giác SABCD có thể tích V, đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm các cạnh SB, BC, CD, DA. Tính thể tích khối chóp M.CNQP theo V.

A. $\frac{3 V}{4}$

B. $\frac{3 V}{8}$

C. $\frac{3 V}{16}$

D. $\frac{V}{16}$

Xem đáp án

Phương pháp:

Công thức tính thể tích khối chóp có diện tích đáy S và chiều cao h là: $V = \frac{1}{3} S h$

Cách giải:

Câu 26:

Cho hàm số f(x) xác định trên R thỏa mãn $f' (x) = 4 x + 3 v à f (1) = - 1$ . Biết rằng phương trình $f (x) = 10$ có hai nghiệm thực $x_{1}, x_{2}$ . Tính tổng $\log_{2} |x_{1}| + \log_{2} |x_{2}|$

A. 8

B. 16

C. 4

D. 3

Xem đáp án

Câu 27:

Cho khai triển ${(\sqrt{3} + x)}^{2019} = a_{0} + a_{1} x + a_{2} x^{2} + a_{3} x^{3} + ..... + a_{2019} x^{2019}$ . Hãy tính tổng $S = a_{0} - a_{2} + a_{4} - a_{6} + ..... + a_{2016} - a_{2018}$

A. ${(\sqrt{3})}^{1009}$

B. 0

C. $2^{2019}$

D. $2^{1009}$

Xem đáp án

Câu 28:

Biết tổng các hệ số trong khai triển nhị thức Newton của ${(5 x - 1)}^{n}$ bằng $2^{100}$ . Tìm hệ số của $x^{3}$

A. $- 161700$

B. -19600

C. -2450000

D. -20212500

Xem đáp án

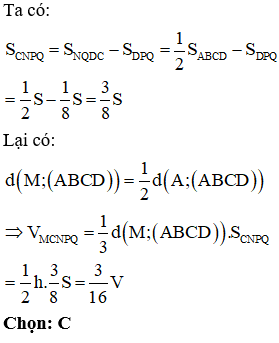
Câu 29:

Số mặt phẳng đối xứng của hình bát diện đều là:

A. 3

B. 5

C. 7

D. 9

Xem đáp án

Phương pháp:

Sử dụng lý thuyết khối đa diện để làm bài toán.

Cách giải:

Hình bát diện đều có 9 mặt phẳng đối xứng.

Chọn: D

Câu 30:

Cho hàm số f(x) liên tục trên R có $\int_{0}^{3} f (x) d x = 8 v à \int_{0}^{5} f (x) d x = 4$ . Tính

A. 3

B. 6

C. $\frac{9}{4}$

D. $\frac{11}{4}$

Xem đáp án

Phương pháp:

Sử dụng phương pháp tích phân đổi biến.

Cách giải:

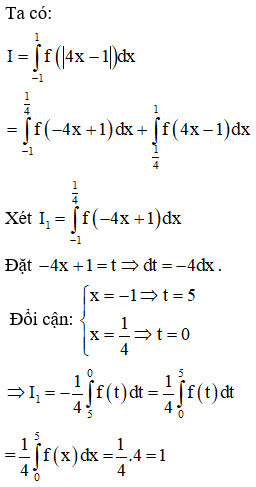
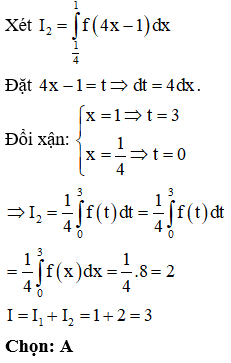
Câu 31:

Cho hai số thực a > 1, b > 1. Gọi $x_{1}, x_{2}$ là hai nghiệm của phương trình $a^{x} b^{x^{2} - 1} = 1$ . Trong trường hợp biểu thức $S = {(\frac{x_{1} x_{2}}{x_{1} + x_{2}})}^{2} - 4 x_{1} - 4 x_{2}$ đạt giá trị nhỏ nhất, mệnh đề nào sau đây là đúng?

A. a < b

B. $a \geq b$

C. ab = 4

D. ab = 2

Xem đáp án

Phương pháp:

+) Lấy loganepe hai vế, đưa phương trình về dạng phương trình bậc hai ẩn x.

+) Tìm điều kiện để phương trình có 2 nghiệm. Áp dụng định lí Vi-ét.

+) Sử dụng BĐT Cô-si cho 3 số không âm đánh giá biểu thức S.

Cách giải:

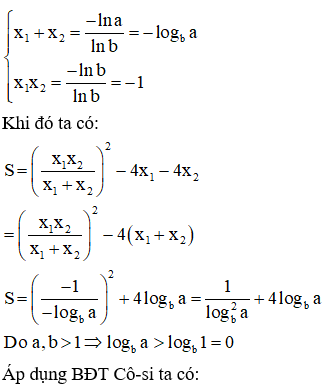
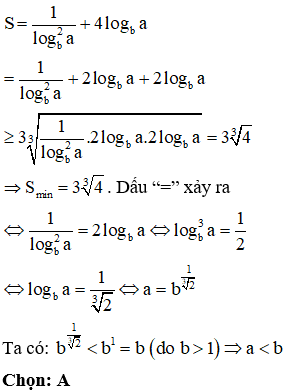
Câu 32:

Cho hình chóp tam giác S.ABC có đáy ABC là một tam giác vuông cân tại B với trọng tâm G, cạnh bên SA tạo với đáy (ABC) một góc $30^{0}$ . Biết hai mặt phẳng $(S B G) v à (S C G)$ cùng vuông góc với mặt phẳng (ABC). Tính cosin của góc giữa hai đường thẳng SA và BC.

A. $\frac{\sqrt{15}}{5}$

B. $\frac{3 \sqrt{15}}{20}$

C. $\frac{\sqrt{15}}{10}$

D. $\frac{\sqrt{30}}{20}$

Xem đáp án

Phương pháp:

+) Gọi M, N, P, Q lần lượt là trung điểm của AB, SC, BC, AC. Chứng minh $∠ (S A; B C) = ∠ (N Q; M Q)$

+) Áp dụng định lí cosin trong tam giác MNQ.

Cách giải:

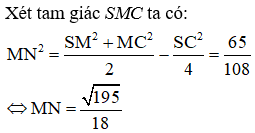
Áp dụng định lý cosin trong tam giác MNQ:

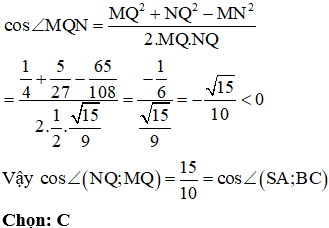
Chú ý: Góc giữa hai đường thẳng là góc nhọn nên cosin của góc giữa hai đường thẳng là giá trị dương.

Câu 33:

Cho hai dãy ghế dối diện nhau, mỗi dãy có 5 ghế. Xếp ngẫu nhiên 10 học sinh, gồm 5 nam, 5 nữ ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Tính xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ.

A. $\frac{1}{252}$

B. $\frac{1}{945}$

C. $\frac{8}{63}$

D. $\frac{1}{63}$

Xem đáp án

Phương pháp:

Xếp lần lượt chỗ ngồi cho từng học sinh nam và nữ sao cho mỗi học sinh nam đều ngồi đối diện với một học sinh nữ. Sử dụng quy tắc nhân.

Cách giải:

Xếp ngẫu nhiên 10 học sinh vào 10 ghế cho 10! cách xếp $\Rightarrow n (Ω) = 10!$

Gọi A là biến cố: “mỗi học sinh nam đều ngồi đối diện với một học sinh nữ”.

+) Xếp học sinh nam thứ nhất vào 1 trong 10 vị trí cho 10 cách xếp.

Chọn 1 trong 5 bạn nữ xếp ngồi đối diện với bạn nam thứ nhất có 5 cách xếp.

+) Xếp bạn nam thứ 2 vào 1 trong 8 vị trí còn lại có 8 cách xếp.

Chọn 1 trong 4 bạn nữ còn lại xếp ngồi đối diện với bạn nam thứ hai có 4 cách xếp.

+) Xếp bạn nam thứ 3 vào 1 trong 6 vị trí còn lại có 6 cách xếp.

Chọn 1 trong 3 bạn nữ còn lại xếp ngồi đối diện với bạn nam thứ ba có 3 cách xếp.

+) Xếp bạn nam thứ 4 vào 1 trong 4 vị trí còn lại có 4 cách xếp.

Chọn 1 trong 2 bạn nữ còn lại xếp ngồi đối diện với bạn nam thứ tư có 2 cách xếp.

+) Xếp bạn nam thứ 5 vào 1 trong 2 vị trí còn lại có 2 cách xếp.

Xếp 1 bạn nữ còn lại vào vị trí cuối cùng có 1 cách xếp.

Câu 34:

Phương trình $\sin x = 2019 x$ có bao nhiêu nghiệm thực?

A. 1288

B. 1287

C. 1290

D. 1289

Xem đáp án

Chọn: B

Câu 35:

Trong không gian với hệ tọa độ Oxyz, gọi $(α)$ là mặt phẳng chứa đường thẳng $d : \frac{x - 2}{1} = \frac{y - 3}{1} = \frac{z}{2}$ và vuông góc với mặt phẳng $(β) : x + y - 2 z + 1 = 0$ . Hỏi giao tuyến của $(α) v à (β)$ là:

A. (1;-2;0)

B. (2;3;3)

C. (5;6;8)

D. (0;1;3)

Xem đáp án

Câu 36:

Cho hàm số $f (x)$ xác định trên R và thỏa mãn $\lim_{x \to 2} \frac{f (x) - 16}{x - 2} = 12$ . Tính giới hạn $\lim_{x \to 2} \frac{\sqrt[3]{5 f (x) - 16} - 4}{x^{2} + 2 x - 8}$

A. $\frac{5}{24}$

B. $\frac{5}{12}$

C. $\frac{1}{4}$

D. $\frac{1}{5}$

Xem đáp án

$\begin{array}{l} = \lim_{x \to 2} \frac{(\sqrt[3]{5 f (x) - 16} - 4) ({\sqrt[3]{5 f (x) - 16}}^{2} + 4 \sqrt[3]{5 f (x) - 16} + 16)}{(x + 4) (x - 2) ({\sqrt[3]{5 f (x) - 16}}^{2} + 4 \sqrt[3]{5 f (x) - 16} + 16)} \\ = \lim_{x \to 2} \frac{5 f (x) - 16 - 64}{(x + 4) (x - 2) ({\sqrt[3]{5 f (x) - 16}}^{2} + 4 \sqrt[3]{5 f (x) - 16} + 16)} \\ = \lim_{x \to 2} \frac{5 [f (x) - 16]}{(x + 4) (x - 2) ({\sqrt[3]{5 f (x) - 16}}^{2} + 4 \sqrt[3]{5 f (x) - 16} + 16)} \\ = \lim_{x \to 2} \frac{f (x) - 16}{x - 2} . \frac{5}{({\sqrt[3]{5 f (x) - 16}}^{2} + 4 \sqrt[3]{5 f (x) - 16} + 16)} \end{array}$

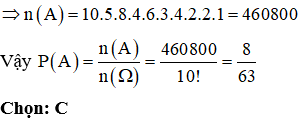
Câu 37:

Cho phương trình $\frac{\cos 4 x - \cos 2 x + 2 \sin^{2} x}{\sin x + \cos x} = 0$ . Tính diện tích đa giác có các đỉnh là các điểm biểu diễn các nghiệm của phương trình trên đường tròn lượng giác.

A. $\frac{\sqrt{2}}{4}$

B. $\frac{\sqrt{2}}{2}$

C. $\sqrt{2}$

D. 2 $\sqrt{2}$

Xem đáp án

+) Giải phương trình, biểu diễn các họ nghiệm trên đường tròn lượng giác.

+) Xác định các điểm và tính diện tích đa giác đó.

Cách giải:

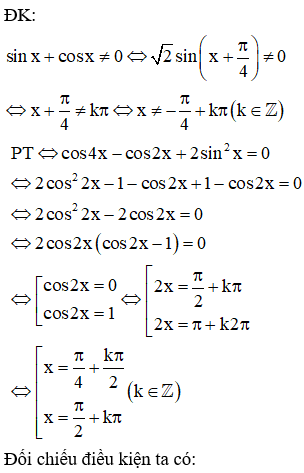
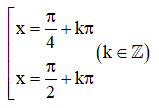
Biểu diễn hai họ nghiệm trên trên đường tròn lượng giác ta được

4 điểm A, B, C, D như sau:

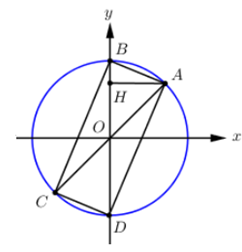
Chú ý: Chú ý đối chiếu điều kiện xác định để loại nghiệm.

Câu 38:

Biết rằng trong không gian với hệ tọa độ Oxyz có hai mặt phẳng (P) và (Q) cùng thỏa mãn các điều kiện sau: đi qua hai điểm $A (1; 1; 1) v à B (0; - 2; 2)$ , đồng thời cắt các trục tọa độ Ox, Oy tại hai điểm cách đều O. Giả sử (P) có phương trình $x + b_{1} y + c_{1} z + d_{1} = 0$ và (Q) có phương trình $x + b_{2} y + c_{2} z + d_{2} = 0$ . Tính giá trị của biểu thức $b_{1} b_{2} + c_{1} c_{2}$

A. -7

B. -9

C. 9

D. 7

Xem đáp án

Câu 39:

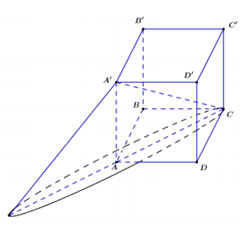
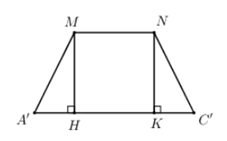
Cho lăng trụ đều $A B C . A' B' C'$ có cạnh đáy bằng a, bạnh bên bằng $\sqrt{2} a$ . Gọi M là trung điểm AB. Tính diện tích thiết diện cắt lăng trụ đã cho bởi mặt phẳng $(A' C' M)$

A. $\frac{9}{8} a^{2}$

B. $\frac{3 \sqrt{2}}{4} a^{2}$

C. $\frac{3 \sqrt{35}}{16} a^{2}$

D. $\frac{7 \sqrt{2}}{16} a^{2}$

Xem đáp án

Phương pháp:

+) Xác định thiết diện dựa vào các yếu tố song song. Chứng minh thiết diện là hình thang cân.

+) Tính diện tích hình thang cân.

Cách giải:

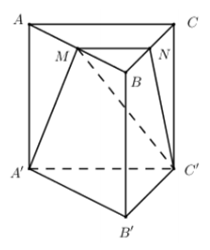
Gọi N là trung điểm của BC ta có MN là đường trung bình của tam giác $A B C \Rightarrow M N / / A C$

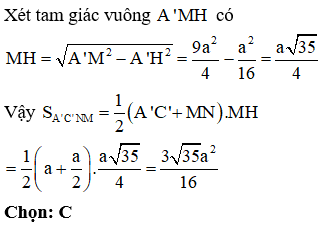
Câu 40:

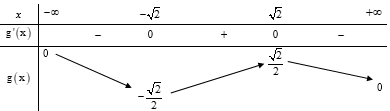
Có bao nhiêu giá trị nguyên của tham số m trong đoạn $[- 2019; 2019]$ để hàm số $y = \ln (x^{2} + 2) - m x + 1$ đồng biến trên R

A. 4038

B. 2019

C. 2020

D. 1009

Xem đáp án

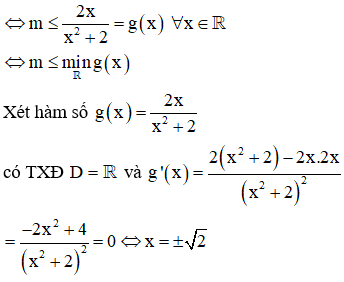
BBT:

Câu 41:

Cho hai số thực thỏa mãn $x^{2} + y^{2} = 1$ . Đặt $P = \frac{x^{2} + 6 x y}{1 + 2 x y + 2 y^{2}}$ . Khẳng định nào sau đây là đúng?

A. Giá trị nhỏ nhất của P là -3

B. Giá trị lớn nhất của P là 1

C. P không có giá trị lớn nhất

D. P không có giá trị nhỏ nhất

Xem đáp án

Chọn: A

Câu 42:

Cho hàm số $f (x) = \{\begin{cases} \frac{\sqrt{3 x + 1} - 2 x}{x - 1} k h i x \neq 1 \\ - \frac{5}{4} k h i x = 1 \end{cases}$ . Tính $f' (1)$

A. 0

B. $- \frac{7}{50}$

C. $- \frac{9}{64}$

D. không tồn tại

Xem đáp án

Phương pháp:

+) Kiểm tra tính liên tục của hàm số tại x = 1

+) Nếu hàm số liên tục tại x = 1, sử dụng công thức tính đạo hàm bằng định nghĩa:

Câu 43:

Trong không gian với hệ tọa độ Oxyz cho hai điểm $A (0; 0; 3), B (- 2; 0; 1)$ và mặt phẳng $(α) : 2 x - y + 2 z + 8 = 0$ . Hỏi có bao nhiêu điểm C trên mặt phẳng $(α)$ sao cho tam giác ABC đều.

A. 2

B. 0

C. 1

D. Vô số

Xem đáp án

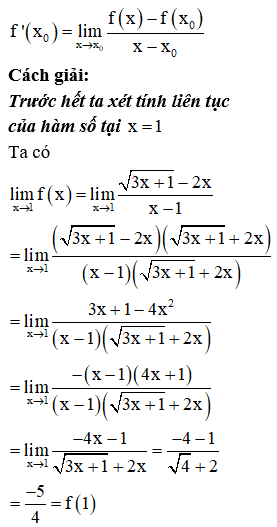
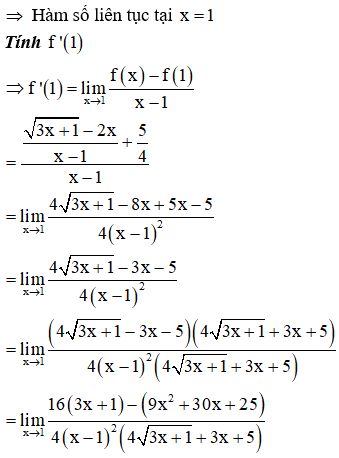
Câu 44:

Gọi (C) là đồ thị hàm số $y = x^{2} + 2 x + 2$ và điểm M di chuyển trên (C). Gọi $d_{1}, d_{2}$ là các đường thẳng đi qua M sao cho $d_{1}$ song song với trục tung và $d_{1}, d_{2}$ đối xứng nhau qua tiếp tuyến của (C) tại M. Biết rằng khi M di chuyển trên (C) thì $d_{2}$ luôn đi qua một điểm $I (a; b)$ cố định. Đẳng thức nào sau đây là đúng?

A. ab = -1

B. a + b = 0

C. 3a + 2b = 0

D. 5a + 4b = 0

Xem đáp án

Chọn: D

Câu 45:

Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a và $∠ S B A = ∠ S C A = 90^{0}$ . Biết góc giữa đường thẳng SA và mặt phẳng ABC bằng $45^{0}$ . Khoảng cách giữa hai đường thẳng SB và AC là:

A. $\frac{2 \sqrt{51}}{17} a$

B. $\frac{2 \sqrt{7}}{7} a$

C. $\frac{\sqrt{39}}{13} a$

D. $\frac{2 \sqrt{13}}{13} a$

Xem đáp án

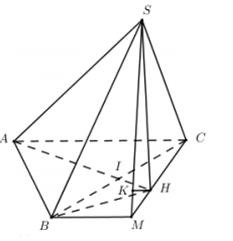
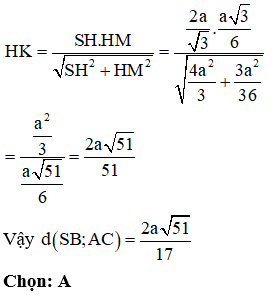
Áp dụng hệ thức lượng trong tam giác vuông SMH ta có:

Câu 46:

Cho hàm số f(x) liên tục trên R và thỏa mãn $\int_{0}^{\frac{π}{2}} \tan x f (\cos^{2} x) d x = \int_{1}^{8} \frac{f (\sqrt[3]{x})}{x} d x = 6$ . Tính tích phân $\int_{\frac{1}{2}}^{\sqrt{2}} \frac{f (x^{2})}{x} d x$

A. 4

B. 6

C. 7

D. 10

Xem đáp án

Chọn: C

Câu 47:

Cho tứ diện ABCD có $A C = A D = B C = B D = a, (A C D) ⊥ (B C D) v à (A B C) ⊥ (A B D)$ . Tính độ dài cạnh CD.

A. $\frac{2 \sqrt{3}}{3} a$

B. $2 \sqrt{2} a$

C. $\sqrt{2} a$

D. $\frac{\sqrt{3}}{3} a$

Xem đáp án

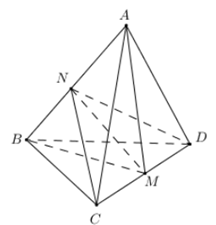
Gọi M, N lần lượt là trung điểm của CD, AB.

Câu 48:

Cho một đa giác đều có 48 đỉnh. Lấy ngẫu nhiên ba đỉnh của đa giác. Tính xác suất để tam giác tạo thành từ ba đỉnh đó là một tam giác nhọn.

A. $\frac{22}{47}$

B. $\frac{11}{47}$

C. $\frac{33}{47}$

D. $\frac{33}{94}$

Xem đáp án

Phương pháp:

Xác suất của biến cố A được tính bởi công thức: $P (A) = \frac{n_{A}}{n_{Ω}}$

Cách giải:

Số cách chọn 3 đỉnh bất kì của đa giác là: $n_{Ω} = C_{48}^{3}$

Gọi O là tâm đường tròn ngoại tiếp đa giác đều.

Gọi biến cố A: “Chọn 3 đỉnh bất kì của đa giác để được một tam giác nhọn”.

Lấy điểm A thuộc đường tròn (O), kẻ đường kính AA’ => A’ cũng thuộc đường tròn (O).

Khi đó AA’ chia đường tròn (O) thành hai nửa, mỗi nửa có 23 đỉnh.

Chọn 2 đỉnh B, C cùng thuộc 1 nửa đường tròn có $C_{23}^{2} c á c h c h ọ n \Rightarrow$ có $C_{23}^{2}$ tam giác ABC là tam giác tù.

Tương tự như vậy đối với nửa còn lại nên ta có 2 $C_{23}^{2}$ tam giác tù được tạo thành.

Đa giác đều có 48 đỉnh nên có 24 đường chéo => có 24.2. $C_{23}^{2}$ tam giác tù.

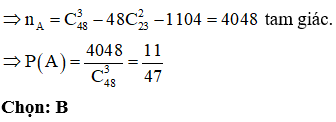
Ứng với mỗi đường kính ta có 23.2 tam giác vuông. Vậy số tam giác vuông là: 23.2.24 = 1104 tam giác.

Câu 49:

Cho hàm số $y = - x^{3} + 3 x^{2} + 9 x$ có đồ thị (C). Gọi A, B, C, D là bốn điểm trên đồ thị (C) với hoành độ lần lượt là a, b, c, d sao cho tứ giác ABCD là một hình thoi đồng thời hai tiếp tuyến tại A, C song song với nhau và đường thẳng AC tạo với hai trục tọa độ một tam giác cân. Tính tích abcd.

A. 144

B. 60

C. 180

D. 120

Xem đáp án

Chọn: D

Câu 50:

Trong không gian với hệ tọa độ Oxyz cho ba điểm $A (8; 5; - 11), B (5; 3; - 4), C (1; 2; - 6)$ và mặt cầu $(S) : {(x - 2)}^{2} + {(y - 4)}^{2} + {(z + 1)}^{2} = 9$ . Gọi điểm $M (a; b; c)$ là điểm trên (S) sao cho $|\vec{M A} - \vec{M B} - \vec{M C}|$ đạt giá trị nhỏ nhất. Hãy tìm a+b

A. 9

B. 4

C. 2

D. 6

Xem đáp án

CHỌN BỘ SÁCH BẠN MUỐN XEM

Tổng hợp 20 đề thi thử thpt quốc gia môn Toán cực hay có lời giải chi tiết abc

Tổng hợp 20 đề thi thử thpt quốc gia môn Toán cực hay có lời giải chi tiết abc - đề 14

Danh sách câu hỏi

Bài thi liên quan