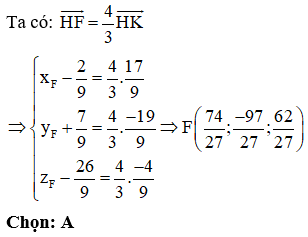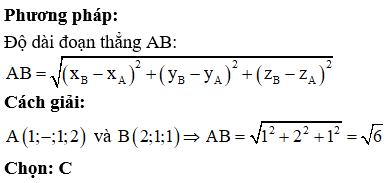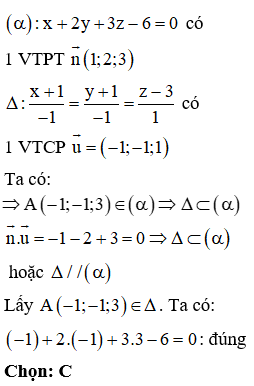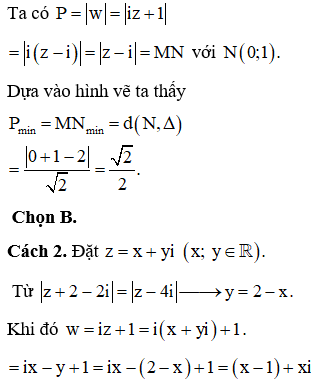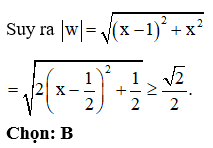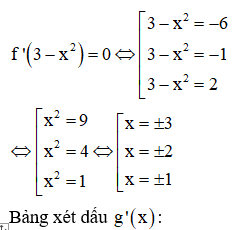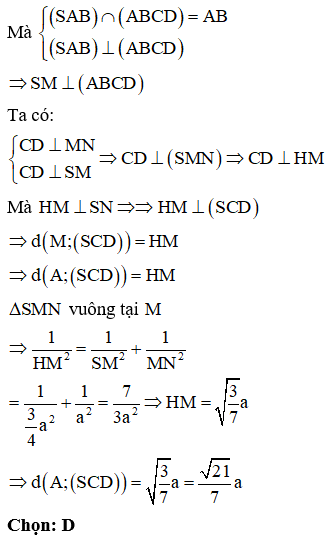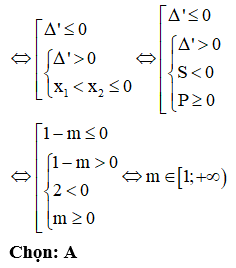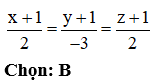50 câu hỏi trắc nghiệm thuộc Tổng hợp 20 đề thi thử thpt quốc gia môn Toán cực hay có lời giải chi tiết abc - đề 13

Câu 1:

Cho cấp số cộng $(u_{n})$ có số hạng đầu $u_{1} = - 3 v à u_{6} = 27$ . Tìm công sai d.

A. d = 8

B. d = 6

C. d = 5

D. d = 7

Xem đáp án

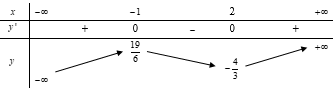
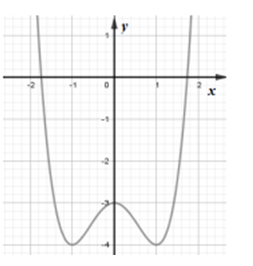
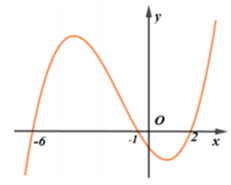
Câu 2:

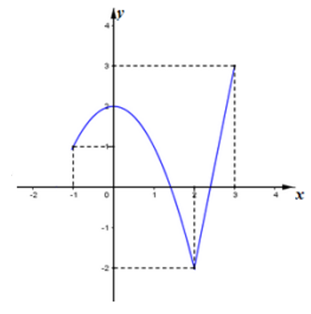
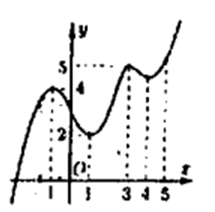
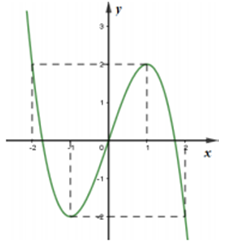
Cho hàm số $y = f (x)$ có đồ thị như hình bên. Giá trị cực tiểu của hàm số đã cho bằng

A. 2

B. -2

C. 1

D. -1

Xem đáp án

Phương pháp:

Dựa vào đồ thị hàm số xác định các điểm cực trị của hàm số.

Cách giải:

Hàm số đạt cực tiểu tại x = -1, giá trị cực tiểu là $y_{C T} = - 2$

Chọn: B

Chú ý: Học sinh hay nhầm lẫn điểm cực tiểu và giá trị cực tiểu của hàm số.

Câu 3:

Cho a là số thực dương tùy ý. Mệnh đề nào sau đây đúng?

A. $\log_{3} \frac{3}{a^{2}} = 3 - 2 \log_{3} a$

B. $\log_{3} \frac{3}{a^{2}} = 1 + 2 \log_{3} a$

C. $\log_{3} \frac{3}{a^{2}} = 3 - \frac{1}{2} \log_{3} a$

D. $\log_{3} \frac{3}{a^{2}} = 1 - 2 \log_{3} a$

Xem đáp án

Câu 4:

Tổng tất cả các nghiệm của phương trình $(x^{2} + 2 x - 3) (\log_{2} x - 3) = 0$ bằng

A. 3

B. 2

C. 9

D. 6

Xem đáp án

Câu 5:

Nếu $\int_{2}^{5} f (x) d x = 3 v à \int_{5}^{7} f (x) d x = 9 t h ì \int_{2}^{7} f (x) d x$ bằng bao nhiêu?

A. -6

B. 6

C. 12

D. 3

Xem đáp án

Câu 6:

Cho hàm số f(x) liên tục trên đoạn [-1;3] và có đồ thị như hình vẽ bên. Gọi M và m lần lượt là GTLN và GTNN của hàm số đã cho trên $[- 1; 3]$ . Giá trị của P = m.M bằng?

A. 3

B. -4

C. 6

D. -4

Xem đáp án

Câu 7:

Cho hàm số f(x) có bảng biến thiên như sau:

Hàm số $y = f (x)$ nghịch biến trên khoảng nào dưới đây?

A. $(- \infty; - 1)$

B. $(- \frac{4}{3}; \frac{19}{6})$

C. $(- 1; + \infty)$

D. $(- 1; 2)$

Xem đáp án

Câu 8:

Họ nguyên hàm của hàm số $f (x) = 2^{x} + x$ là

A. $\frac{2^{x}}{\ln 2} + \frac{1}{2} x^{2} + C$

B. $2^{x} . l n 2 + \frac{1}{2} x^{2} + C$

C. $2^{x} + \frac{1}{2} x^{2} + C$

D. $2^{x} + 1 + C$

Xem đáp án

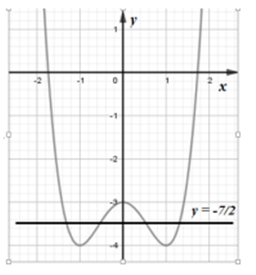
Câu 9:

Điểm A trong hình vẽ bên là điểm biểu diễn của số phức z. Khi đó

mệnh đề nào sau đây là đúng?

A. $\bar{z} = 1 + 2 i$

B. $\bar{z} = 2 + 2 i$

C. $\bar{z} = 2 - i$

D. $\bar{z} = 2 + i$

Xem đáp án

Câu 10:

Trong không gian Oxyz, mặt phẳng (Oyz) có phương trình là:

A. x + y + z = 0

B. z = 0

C. y = 0

D. x = 0

Xem đáp án

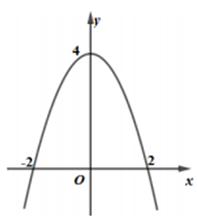
Câu 11:

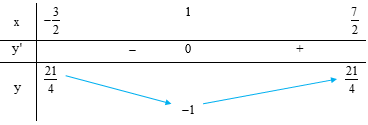
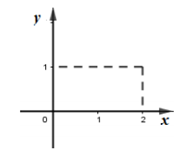
Đồ thị như hình vẽ là của hàm số

A. $y = x^{3} - 3 x^{2} + 1$

B. $y = - \frac{x^{3}}{3} + x^{2} + 1$

C. $y = x^{4} + 3 x^{2} + 1$

D. $y = 3 x^{2} + 2 x + 1$

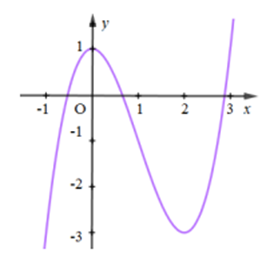
Xem đáp án

Phương pháp:

Nhận biết đồ thị hàm số bậc ba.

Cách giải:

Quan sát đồ thị hàm số ta thấy: đây không phải đồ thị hàm số bậc 4 trùng phương và hàm số bậc 2.

=> Loại phương án C và D.

Câu 12:

Trong không gian Oxyz, cho mặt phẳng $(P) : 2 x - y + z - 1 = 0$ đi qua điểm nào dưới đây?

A. $M (2; - 1; 1)$

B. $P (1; - 2; 0)$

C. $Q (1; - 3; - 4)$

D. $N (0; 1; - 2)$

Xem đáp án

Phương pháp:

Thay tọa độ các điểm vào phương trình (P), xác định điểm có tọa độ thỏa mãn phương trình.

Cách giải:

Câu 13:

Trong không gian Oxyz, cho hai điểm $A (1; - 1; 2) v à B (2; 1; 1)$ . Độ dài đoạn AB bằng

A. $3 \sqrt{2}$

B. 18

C. $\sqrt{6}$

D. 6

Xem đáp án

Câu 14:

Diện tích của mặt cầu có đường kính 3m là:

A. $9 π (m^{2})$

B. $3 π (m^{2})$

C. $12 π (m^{2})$

D. $36 π (m^{2})$

Xem đáp án

Câu 15:

Gọi S là tập hợp những số có dạng $\bar{x y z}$ với $x, y, z \in \{1; 2; 3; 4; 5\}$ . Số phần tử của tập hợp S là:

A. 5!

B. $A_{5}^{3}$

C. $C_{5}^{3}$

D. $5^{3}$

Xem đáp án

Phương pháp:

Sử dụng quy tắc nhân.

Cách giải:

Mỗi chữ số x, y, z đều có 5 cách chọn suy ra số phần tử của tập hợp S là: $5^{3}$

Chọn: D

Câu 16:

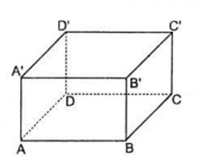
Tính thể tích của khối hộp chữ nhật $A B C D . A' B' C' D' c ó A B = 3, A C = 5, A A' = 5$

A. 40

B. 75

C. 60

D. 70

Xem đáp án

Phương pháp:

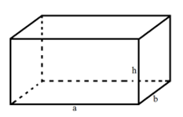
Thể tích của khối hộp chữ nhật có số đo như hình vẽ: V = a.b

Cách giải:

Câu 17:

Tổng tất cả các nghiệm của phương trình $\log_{2} ({3.2}^{x} - 1) = 2 x + 1$ bằng

A. $\frac{1}{2}$

B. $\frac{3}{2}$

C. -1

D. 0

Xem đáp án

Câu 18:

Trong không gian Oxyz, cho mặt phẳng $(α) : x + 2 y + 3 z - 6 = 0$ và đường thẳng $Δ : \frac{x + 1}{- 1} = \frac{y + 1}{- 1} = \frac{z - 3}{1}$ . Mệnh đề nào sau đây đúng?

A. $Δ ⊥ (α)$

B. $∆ c ắ t v à k h ô n g v u ô n g g ó c v ớ i (α)$

C. $Δ \subset (α)$

D. $Δ / / (α)$

Xem đáp án

Câu 19:

Gọi F(x) là một nguyên hàm của hàm số $f (x) = x e^{- x}$ . Tính F(x) biết $F (0) = 1$

A. $F (x) = - (x + 1) e^{- x} + 1$

B. $F (x) = (x + 1) e^{- x} + 2$

C. $F (x) = (x + 1) e^{- x} + 1$

D. $F (x) = - (x + 1) e^{- x} + 2$

Xem đáp án

Câu 20:

Người ta xây một bể nước hình trụ (tham khảo hình vẽ bên) có bán kính R = 1m (tính từ tâm bể đến mép ngoài), chiều dày của thành bể là $b = 0, 05 m$ , chiều cao của bể là $h = 1, 5 m$ . Tính dung tích của bể nước (làm tròn đến hai chữ số thập phân).

A. 4,26 $(m^{3})$

B. 4,25 $(m^{3})$

C. 4,27 $(m^{3})$

D. 4,24 $(m^{3})$

Xem đáp án

Câu 21:

Tính diện tích xung quanh của hình nón có chiều cao h = 8 cm, bán kính đường tròn đáy r = 6 cm.

A. $120 π (c m^{2})$

B. $180 π (c m^{2})$

C. $360 π (c m^{2})$

D. $60 π (c m^{2})$

Xem đáp án

Câu 22:

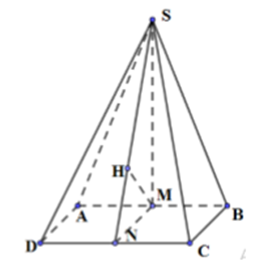
Cho hình chóp S.ABC có đáy là tam giác vuông tại B. Biết $Δ S A B$ đều và thuộc mặt phẳng vuông góc với mặt phẳng $(A B C)$ . Tính theo a thể tích khối chóp S.ABC biết $A B = a, A C = a \sqrt{3}$

A. $\frac{a^{3} \sqrt{2}}{6}$

B. $\frac{a^{3}}{4}$

C. $\frac{a^{3} \sqrt{6}}{12}$

D. $\frac{a^{3} \sqrt{6}}{4}$

Xem đáp án

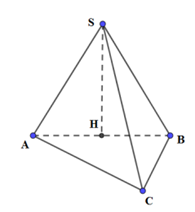
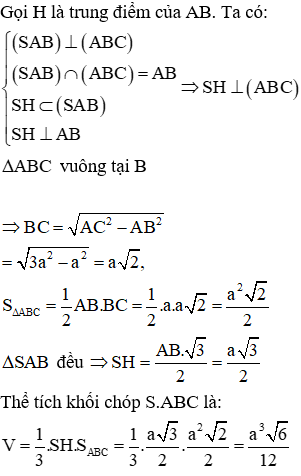
Chọn: C

Câu 23:

Tính đạo hàm của hàm số $y = (x^{2} - 2 x + 2) e^{x}$

A. $y' = (2 x - 2) e^{x}$

B. $y' = (x^{2} + 2) e^{x}$

C. $y' = x^{2} e^{x}$

D. $y' = - 2 x e^{x}$

Xem đáp án

Câu 24:

Cho hàm số f(x) có đạo hàm $f' (x) = (x - 1) (x^{2} - 4) (x^{3} - 1), \forall x \in ℝ$ . Số điểm cực trị của hàm số đã cho là

A. 1

B. 4

C. 2

D. 3

Xem đáp án

Câu 25:

Gọi $z_{1}, z_{2}$ là nghiệm của phương trình $z^{2} - 2 z + 4 = 0$ . Tính giá trị của biểu thức $P = \frac{z_{1}^{2}}{z_{2}} + \frac{z_{2}^{2}}{z_{1}}$

A. $- \frac{11}{4}$

B. 4

C. -4

D. 8

Xem đáp án

Câu 26:

Cho hình chóp tứ giác đều có cạnh đáy bằng a và chiều cao bằng $\frac{a \sqrt{3}}{2}$ . Tính số đo góc giữa mặt bên và mặt đáy.

A. $60^{0}$

B. $30^{0}$

C. $75^{0}$

D. $45^{0}$

Xem đáp án

Phương pháp:

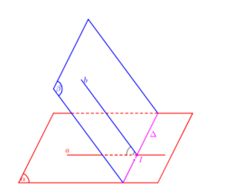
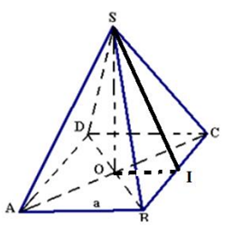
Gọi O là tâm của hình vuông ABCD. I là trung điểm của BC. Ta có:

Câu 27:

Cho hàm số f(x) liên tục trên $ℝ$ và có đồ thị như hình bên. Số nghiệm dương phân biệt của phương trình $2 f (x) + 7 = 0$ là

A. 1

B. 4

C. 2

D. 3

Xem đáp án

Câu 28:

Cho $a = \log_{2} 5, b = \log_{2} 9$ . Khi đó $P = \log_{2} \frac{40}{3}$ tính theo a và b là

A. $P = 3 + a - 2 b$

B. $P = 3 + a - \frac{1}{2} b$

C. $P = 3 + a - \sqrt{b}$

D. $P = \frac{3 a}{2 b}$

Xem đáp án

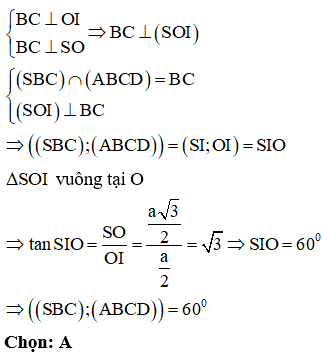
Câu 29:

Trong không gian Oxyz, cho hai điểm $A (- 2; 1; 0), B (2; - 1; 2)$ . Phương trình của mặt cầu có đường kính AB là:

A. $x^{2} + y^{2} + {(z - 1)}^{2} = 24$

B. $x^{2} + y^{2} + {(z - 1)}^{2} = 6$

C. $x^{2} + y^{2} + {(z - 1)}^{2} = \sqrt{24}$

D. $x^{2} + y^{2} + {(z - 1)}^{2} = \sqrt{6}$

Xem đáp án

Chọn: B

Câu 30:

Cho Parabol như hình vẽ bên. Diện tích hình phẳng giới hạn bởi Parabol và trục hoành bằng

A. 16

B. $\frac{32}{3}$

C. $\frac{16}{3}$

D. $\frac{28}{3}$

Xem đáp án

Câu 31:

Tập nghiệm S của bất phương trình ${(\frac{1}{2})}^{x^{2} - 4 x} < 8$ là

A. $S = (1; + \infty)$

B. $S = (1; 3)$

C. $S = (- \infty; 3)$

D. $S = (- \infty; 1) \cup (3; + \infty)$

Xem đáp án

Câu 32:

Cho hàm số $y = f (x)$ có bảng biến thiên như sau:

Số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là:

A. 4

B. 1

C. 2

D. 3

Xem đáp án

Câu 33:

Cho hai số thực a và b thỏa mãn: $(1 + i) z + (2 - i) \bar{z} = 13 + 2 i$ với i là đơn vị ảo

A. $a = - 3, b = 2$

B. $a = - 3, b = - 2$

C. $a = 3, b = - 2$

D. $a = 3, b = 2$

Xem đáp án

Câu 34:

Cho số phức z thỏa mãn $(z - 2 + i) (\bar{z} - 2 - i) = 25$ . Biết tập hợp các điểm M biểu diễn số phức $w = 2 \bar{z} - 2 + 3 i$ là đường tròn tâm $I (a; b)$ và bán kính c. Giá trị của $a + b + c$ bằng

A. 10

B. 18

C. 17

D. 20

Xem đáp án

Ta có:

$A (2; - 1) \underset{⇁}{Đ_{(O x)}} B (2; 1) \underset{⇁}{V_{(O (0; 0); k = 2)}} C (4; 2) \underset{⇁}{T_{\vec{u} (- 2; 3)}} D (2; 5)$

Câu 35:

Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ bên.

Có bao nhiêu giá trị nguyên của tham số m để phương trình $f (x^{2} - 2 x) = m$ có đúng 4 nghiệm thực phân biệt thuộc đoạn $[- \frac{3}{2}; \frac{7}{2}]$ ?

A. 3

B. 1

C. 4

D. 2

Xem đáp án

Câu 36:

Cho $\int_{0}^{1} \frac{x d x}{{(2 x + 1)}^{2}} = a + b \ln 2 + c \ln 3$ với a, b, c là các số hữu tỉ. Giá trị của $a + b + c$ bằng:

A. $\frac{5}{12}$

B. $\frac{1}{12}$

C. $- \frac{1}{3}$

D. $\frac{1}{4}$

Xem đáp án

Chú ý: Chú ý khi sử dụng các nguyên hàm mở rộng.

Câu 37:

Xét các số phức z, w thỏa mãn $|z + 2 - 2 i| = |z - 4 i|$ và $w = i z + 1$ . Giá trị nhỏ nhất của $|w|$ bằng?

A. 2

B. $\frac{\sqrt{2}}{2}$

C. $\frac{3 \sqrt{2}}{2}$

D. $2 \sqrt{2}$

Xem đáp án

Câu 38:

Cho hàm số $y = f (x)$ thỏa mãn $f' (x) = - x^{2} - 4, \forall x \in ℝ$ . Bất phương tình $f (x) < m$ có nghiệm thuộc khoảng $(- 1; 1)$ khi và chỉ khi

A. $m > f (1)$

B. $m > f (- 1)$

C. $m \geq f (1)$

D. $m \geq f (- 1)$

Xem đáp án

Câu 39:

Cho hàm số $y = f (x)$ . Đồ thị hàm số $y = f' (x)$ như hình bên. Hỏi hàm số $g (x) = f (3 - x^{2})$ đồng biến trong khoảng nào trong các khoảng sau?

A. (-1;0)

B. (0;1)

C. (2;3)

D. (-2;-1)

Xem đáp án

Câu 40:

Ông An xây dựng một sân bóng đá mini hình chữ nhật có chiều rộng 30m và chiều dài 50m. Để giảm bớt chi phí cho việc trồng cây nhân tạo, ông An chia sân bóng ra làm hai phần (tô đen và không tô đen) như hình bên. Phần tô đen gồm hai miền diện tích bằng nhau và đường cong AIB là một parabol đỉnh I. Phần tô đen được trồng cỏ nhân tạo với giá 130 000 đồng/m2 và phần còn lại được trồng cỏ nhân tạo với giá 90 000 đồng/m2. Hỏi ông An phải trả bao nhiêu tiền để trồng cỏ nhân tạo cho sân bóng?

A. 151 triệu đồng

B. 165 triệu đồng

C. 195 triệu đồng

D. 143 triệu đồng

Xem đáp án

Câu 41:

Ngày 01 tháng 01 năm 2019, ông An gửi 800 triệu đồng vào một ngân hàng với lãi suất 0;5%/tháng. Từ đó, cứ tròn mỗi tháng ông đến ngân hàng rút 6 triệu để chi tiêu cho gia đình. Hỏi đến ngày 01 tháng 01 năm 2020, sau khi rút tiền, số tiền tiết kiệm của ông An còn lại bao nhiêu? Biết rằng lãi suất trong suốt thời gian gửi không thay đổi.

A. $1200 - 400. {(1, 005)}^{11}$ (triệu đồng)

B. $800. {(1, 005)}^{11} - 72$ (triệu đồng)

C. $800. {(1, 005)}^{12} - 72$ (triệu đồng)

D. $1200 - 400. {(1, 005)}^{12}$ (triệu đồng)

Xem đáp án

Câu 42:

Sắp xếp 12 học sinh của lớp 12A gồm 6 học sinh nam và 6 học sinh nữ vào một dàn gồm có hai dãy ghế đối diện nhau (mỗi dãy gồm 6 chiếc ghế) để thảo luận nhóm. Tính xác suất để hai học sinh ngồi đối diện nhau và cạnh nhau luôn khác giới.

A. $\frac{1}{665280}$

B. $\frac{1}{462}$

C. $\frac{1}{924}$

D. $\frac{3}{99920}$

Xem đáp án

Nam	Nữ	Nam	Nữ	Nam	Nữ
Nữ	Nam	Nữ	Nam	Nữ	nam

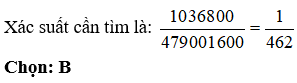
Số cách để hai học sinh ngồi đối diện nhau và cạnh nhau luôn khác giới là: 400.2592 = 1036800 (cách)

Số phần tử của không gian mẫu là: 12! = 479001600

Câu 43:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính theo a khoảng cách từ điểm A đến mặt phẳng $(S C D)$ được kết quả

A. 3a

B. $\frac{a \sqrt{15}}{5}$

C. $\frac{a \sqrt{3}}{7}$

D. $\frac{a \sqrt{21}}{7}$

Xem đáp án

Câu 44:

Tập hợp tất cả các giá trị thực của tham số m để hàm số $y = - \frac{1}{3} x^{3} + x^{2} - m x + 1$ nghịch biến trên khoảng $(0; + \infty)$ là:

A. $m \in [1; + \infty)$

B. $m \in [0; + \infty)$

C. $m \in (0; + \infty)$

D. $m \in (1; + \infty)$

Xem đáp án

Câu 45:

Trong không gian Oxyz, cho mặt phẳng $(P) : x + 2 y + 2 z + 5 = 0$ và đường thẳng $d : \frac{x - 1}{2} = \frac{y - 1}{2} = \frac{z}{1}$ . Đường thẳng $Δ$ nằm trong mặt phẳng (P), đồng thời vuông góc và cắt đường thẳng d có phương trình là:

A. $\frac{x + 1}{2} = \frac{y + 1}{3} = \frac{z + 1}{2}$

B. $\frac{x + 1}{2} = \frac{y + 1}{- 3} = \frac{z + 1}{2}$

C. $\frac{x - 1}{2} = \frac{y + 1}{- 3} = \frac{z - 1}{2}$

D. $\frac{x - 1}{- 2} = \frac{y - 1}{3} = \frac{z - 1}{- 2}$

Xem đáp án

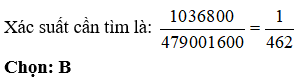
Câu 46:

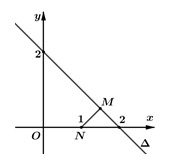
Cho x, y là hai số thực dương thỏa mãn $4 + {9.3}^{x^{2} - 2 y} = (4 + 9^{x^{2} - 2 y}) {.7}^{2 y - x^{2} + 2}$ . Giá trị nhỏ nhất của biểu thức $P = \frac{x + 2 y + 18}{x}$ bằng

A. 9

B. $\frac{3 + \sqrt{2}}{2}$

C. $1 + 9 \sqrt{2}$

D. 17

Xem đáp án

Chọn: A

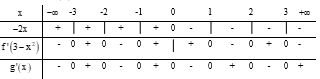
Câu 47:

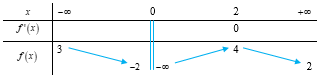
Cho hàm số $y = f (x)$ liên tục trên đoạn $[1; 3]$ và có bảng biến thiên như sau:

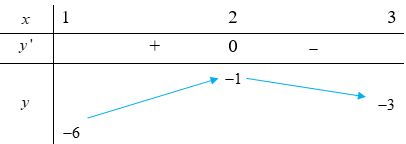
Tổng các giá trị $m \in ℤ$ sao cho phương trình $f (x - 1) = \frac{m}{x^{2} - 6 x + 12}$ có hai nghiệm phân biệt trên đoạn [2;4] bằng

A. -75

B. -72

C. -294

D. -297

Xem đáp án

Phương pháp:

Sử dụng phương pháp khảo sát hàm số.

Cách giải:

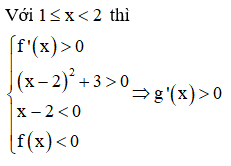
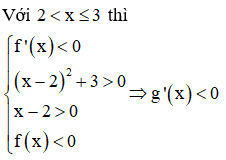
Ta có bảng biến thiên của g(x) như sau:

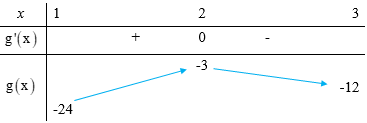
Câu 48:

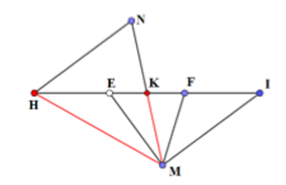
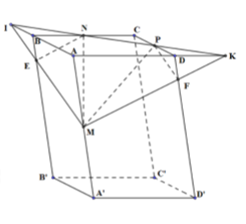
Trong không gian Oxyz, cho mặt phẳng $(P) : 2 x + 2 y - z + 4 = 0$ và các điểm $A (2; 1; 2), B (3; - 2; 2)$ . Điểm M thuộc mặt phẳng (P) sao cho các đường thẳng MA, MB luôn tạo với mặt phẳng (P) một góc bằng nhau. Biết rằng điểm M luôn thuộc đường tròn (C) cố định. Tìm tọa độ tâm của đường tròn (C).

A. $(\frac{74}{27}; - \frac{97}{27}; \frac{62}{27})$

B. $(\frac{32}{9}; - \frac{49}{9}; \frac{2}{9})$

C. $(\frac{10}{3}; - 3; \frac{14}{3})$

D. $(\frac{17}{21}; - \frac{17}{21}; \frac{17}{21})$

Xem đáp án

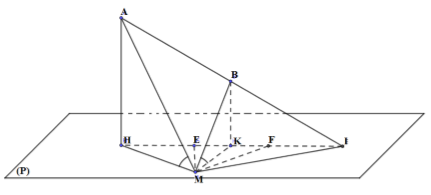
Lấy I đối xứng H qua K; E thuộc đoạn HK sao cho HE = 2KE; F thuộc đoạn KI sao cho FI = 2KF.

Khi đó: A, B, I, H, E, K, F đều là các điểm cố định.

* Ta chứng minh: M di chuyển trên đường tròn tâm F, đường kính IE:

Câu 49:

Trong không gian Oxyz, cho $A (1; 1; - 1), B (- 1; 2; 0), C (3; - 1; - 2)$ . Giả sử $M (a; b; c)$ thuộc mặt cầu $(S) : {(x - 1)}^{2} + y^{2} + {(z + 1)}^{2} = 861$ sao cho $P = 2 M A^{2} - 7 M B^{2} + 4 M C^{2}$ đạt giá trị nhỏ nhất. Giá trị $T = |a| + |b| + |c|$ bằng

A. T = 47

B. T = 55

C. T = 51

D. T = 49

Xem đáp án

Câu 50:

Cho hình hộp $A B C D . A' B' C' D'$ . Gọi M, N, P lần lượt là trung điểm của $A A', B C, C D$ . Mặt phẳng $(M N P)$ chia khối hộp thành hai phần có thể tích là $V_{1}, V_{2}$ . Gọi $V_{1}$ là thể tích phần chứa điểm C. Tỉ số $\frac{V_{1}}{V_{2}}$ bằng

A. $\frac{119}{25}$

B. $\frac{3}{4}$

C. $\frac{113}{24}$

D. $\frac{119}{425}$

Xem đáp án

CHỌN BỘ SÁCH BẠN MUỐN XEM

Tổng hợp 20 đề thi thử thpt quốc gia môn Toán cực hay có lời giải chi tiết abc

Tổng hợp 20 đề thi thử thpt quốc gia môn Toán cực hay có lời giải chi tiết abc - đề 13

Danh sách câu hỏi

Bài thi liên quan