Giải sách bài tập Toán lớp 10 Bài 2: Tập hợp

Bài 1 trang 13 SBT Toán 10 Tập 1: Viết các tập hợp sau đây dưới dạng liệt kê các phần tử:

a) A = {x | x² – 2x – 15 = 0};

b) B = {x ∈ ℤ | – 3 < x ≤ 2};

c) C = $\left\{\frac{n}{n^2-1}|n\in \mathbb{N},1<n\le 4\right\}$;

d) D = {(x; y) | x ≤ 2, y < 2, x, y ∈ ℕ}.

Lời giải:

a) Giải phương trình x² – 2x – 15 = 0 ta được hai nghiệm là x = – 3 và x = 5.

Do đó, A = {– 3; 5}.

b) Vì x ∈ ℤ và – 3 < x ≤ 2 nên x là các số nguyên lớn hơn – 3 và nhỏ hơn hoặc bằng 2, đó là các số: – 2; – 1; 0; 1; 2.

Do đó, B = {– 2; – 1; 0; 1; 2}.

c) Ta có n là số tự nhiên lớn hơn 1 và nhỏ hơn hoặc bằng 4, đó là các số: 2; 3; 4.

Với n = 2, ta có $\frac{n}{n^2-1}=\frac{2}{2^2-1}=\frac{2}{4-1}=\frac{2}{3}$.

Với n = 3, ta có $\frac{n}{n^2-1}=\frac{3}{3^2-1}=\frac{3}{9-1}=\frac{3}{8}$.

Với n = 4, ta có $\frac{n}{n^2-1}=\frac{4}{4^2-1}=\frac{4}{16-1}=\frac{4}{15}$.

Do đó, C = $\left\{\frac{2}{3};\frac{3}{8};\frac{4}{15}\right\}$.

d) Ta có x và y là các số tự nhiên, x nhỏ hơn hoặc bằng 2 nên x là các số 0; 1; 2, y nhỏ hơn 2 nên y là các số 0; 1.

Vậy ta có các cặp số (x; y) thỏa mãn D là: (0; 0); (0; 1); (1; 0); (1; 1); (2; 0); (2; 1).

Do đó, D = {(0; 0); (0; 1); (1; 0); (1; 1); (2; 0); (2; 1)}.

Bài 2 trang 13 SBT Toán 10 Tập 1: Viết các tập hợp sau đây bằng cách chỉ ra tính chất đặc trưng của các phần tử:

a) A = {– 4; – 3; – 2; – 1; 0; 1; 2; 3; 4};

b) B = {0; 2; 4; 6; 8; 10};

c) C = $\left\{1;\frac{1}{2};\frac{1}{3};\frac{1}{4};\frac{1}{5}\right\}$;

d) Tập hợp D các số thực lớn hơn hoặc bằng 3 và bé hơn 8.

Lời giải:

a) Các số – 4; – 3; – 2; – 1; 0; 1; 2; 3; 4 là các số nguyên lớn hơn hoặc bằng – 4 và bé hơn hoặc bằng 4.

Do đó, A = {x ∈ ℤ | – 4 ≤ x ≤ 4}.

Ngoài ra, ta có thể viết tập hợp A bằng các cách như sau:

A = {x ∈ ℤ | |x| ≤ 4} hoặc A = {x ∈ ℤ | |x| < 5}.

b) Các số 0; 2; 4; 6; 8; 10 là các số tự nhiên chẵn nhỏ hơn hoặc băng 10.

Do đó, B = {x | x ∈ ℕ, x chẵn, x ≤ 10} hoặc B = {x | x = 2k, k = 0; 1; 2; 3; 4; 5}.

 c) Ta có: 1 = $\frac{1}{1}$.

Do đó, C = $\left\{\frac{1}{n}|n=1;2;3;4;5\right\}$ hoặc C = $\left\{x|x=\frac{1}{n},n\in \mathbb{N},1\le n\le 5\right\}$.

d) D là tập hợp các số thực lớn hơn hoặc bằng 3 và bé hơn 8.

Do đó, D = {x ∈ ℝ | 3 ≤ x < 8}.

Bài 3 trang 13 SBT Toán 10 Tập 1: Điền kí hiệu (∈, ∉, ⊂, ⊄, =) thích hợp vào chỗ chấm.

a) 0 ... {0; 1; 2};

b) {0; 1} ... ℤ;

c) 0 ... {x | x² = 0};

d) {0} ... {x | x² = x};

e) ∅ ... {x ∈ ℝ | x² + 4 = 0};

g) {4; 1} ... {x | x² – 5x + 4 = 0};

h) {n; a; m} ... {m; a; n};

i) {nam} ... {n; a; m}.

Lời giải:

Kí hiệu ∈ (thuộc), ∉ (không thuộc) dùng để chỉ mối quan hệ giữa phần tử và tập hợp.

Kí hiệu ⊂ (tập con), ⊄ (không là tập con) dùng để chỉ mối quan hệ giữa hai tập hợp.

Kí hiệu = dùng để chỉ hai phần tử bằng nhau hoặc hai tập hợp bằng nhau.

a) 0 là một phần tử của tập {0; 1; 2}.

Do đó, 0 ∈ {0; 1; 2}.

b) {0; 1} là một tập hợp gồm hai phần tử là các số nguyên 0; 1 nên {0; 1} là tập con của tập số nguyên ℤ.

Do đó, {0; 1} ⊂ ℤ.

c) Ta có: x² = 0 ⇔ x = 0 nên {x | x² = 0} = {0}.

Do đó, 0 ∈ {x | x² = 0}.

d) Ta có: x² = x ⇔ x² – x = 0 ⇔ x(x – 1) = 0 ⇔ x = 0 hoặc x = 1.

Suy ra {x | x² = x} = {0; 1}.

Tập hợp {0} chứa phần tử 0 là một phần tử của tập hợp {0; 1}.

Do đó, {0} ⊂ {x | x² = x}.

e) Với mọi số thực x, ta có x² + 4 > 0 nên phương trình x² + 4 = 0 vô nghiệm.

Suy ra {x ∈ ℝ | x² + 4 = 0} = ∅.

Hay ∅ = {x ∈ ℝ | x² + 4 = 0}.

g) Ta có: x² – 5x + 4 = 0 ⇔ x² – x – 4x + 4 = 0

⇔ x(x – 1) – 4(x – 1) = 0 ⇔ (x – 1)(x – 4) = 0 ⇔ x = 1 hoặc x = 4.

Suy ra {x | x² – 5x + 4 = 0} = {1; 4}.

Hay {4; 1} = {x | x² – 5x + 4 = 0}.

h) Hai tập hợp {m; a; n} và {m; a; n} đều có các phần tử giống nhau nên đây là hai tập hợp bằng nhau.

Do đó, {n; a; m} = {m; a; n}.

i) Tập hợp {nam} gồm một phần tử là nam, tập hợp {n; a; m} gồm ba phần tử là n, a, m, khác phần tử nam.

Do đó, {nam} ⊄ {n; a; m}.

Bài 4 trang 13 SBT Toán 10 Tập 1: Điền kí hiệu (⊂, ⊃, =) thích hợp vào chỗ chấm.

a) {x | x(x – 1)(x + 1) = 0} ... {x | |x| < 2, x ∈ ℤ};

b) {3; 6; 9} ... {x ∈ ℕ | x là ước của 18};

c) {x | x = 5k, k ∈ ℕ} ... { x ∈ ℕ | x là bội của 5};

d) {4k | k ∈ ℕ} ... {x | x = 2m, m ∈ ℕ}.

Lời giải:

a) Ta có: x(x – 1)(x + 1) = 0 ⇔ x = 0 hoặc x = 1 hoặc x = – 1.

Do đó, {x | x(x – 1)(x + 1) = 0} = {– 1; 0; 1}.         (1)

Lại có: các số nguyên x, sao cho |x| < 2 thì |x| = 0, |x| = 1 hay x = 0, x = 1, x = – 1.

Do đó, {x | |x| < 2, x ∈ ℤ} = {– 1; 0; 1}.        (2)

Từ (1) và (2) suy ra {x | x(x – 1)(x + 1) = 0} = {x | |x| < 2, x ∈ ℤ}.

b) Các số tự nhiên là ước của 18 là: 0; 2; 3; 6; 9; 18.

Do đó, {x ∈ ℕ | x là ước của 18} = {0; 2; 3; 6; 9; 18}.

Vậy {3; 6; 9} ⊂ {x ∈ ℕ | x là ước của 18}.

c) Ta có: x = 5k, k ∈ ℕ, do đó x là các số tự nhiên chia hết cho 5 hay x là bội của 5.

Do đó, {x | x = 5k, k ∈ ℕ} = { x ∈ ℕ | x là bội của 5}.

d) Tập hợp {4k | k ∈ ℕ} gồm các số tự nhiên chia hết cho 4, tập hợp {x | x = 2m, m ∈ ℕ} gồm các số tự nhiên chia hết cho 2. Một số tự nhiên chia hết cho 4 thì chia hết cho 2, nhưng một số tự nhiên chia hết cho 2 thì chưa chắc đã chia hết cho 4.

Do đó, {4k | k ∈ ℕ} ⊂ {x | x = 2m, m ∈ ℕ}.

Bài 5 trang 13 SBT Toán 10 Tập 1: Hãy chỉ ra các quan hệ bao hàm giữa các tập hợp sau và vẽ biểu đồ Ven để biểu diễn các quan hệ đó:

A = {x | x là tứ giác};

B = {x | x là hình vuông};

C = {x | x là hình chữ nhật};

D = {x | x là hình bình hành}.

Lời giải:

Ta có hình vuông, hình chữ nhật, hình bình hành đều là các tứ giác nên các tập hợp B, C, D đều là tập con của tập A.

Do đó ta có các quan hệ bao hàm, B ⊂ A, C ⊂ A, D ⊂ A.          (1)

Lại có hình chữ nhật là hình bình hành nên các phần tử của tập hợp C đều là phần tử của tập hợp D, do đó C ⊂ D.       (2).

Mà hình vuông là hình chữ nhật nên các phần tử của tập hợp B đều là các phần tử của tập hợp C, do đó B ⊂ C.     (3)

Từ (1), (2), (3) và theo tính chất bắc cầu, ta suy ra quan hệ bao hàm: B ⊂ C ⊂ D ⊂ A.

Ta vẽ biểu đồ Ven như sau:

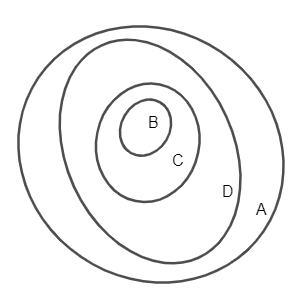
Bài 6 trang 13 SBT Toán 10 Tập 1: Tìm tất cả các tập hợp A thỏa mãn điều kiện {a; b} ⊂ A ⊂ {a; b ; c; d}. 

Lời giải:

Ta có: {a; b} ⊂ A nên tập hợp {a; b} là tập con của tập hợp A, do đó các phần tử của tập {a; b} đều là phần tử của tập A hay a, b là các phần tử của tập A.

Mà A ⊂ {a; b; c; d} nên tập A là tập con của tập {a; b; c; d}, do đó các phần tử của tập A đều là các phần tử của tập {a; b; c; d}, mà tập {a; b; c; d} gồm các phần tử là a, b, c, d, trong đó có a, b là các phần tử của tập A, do đó c, d có thể là các phần tử của tập A.

Vậy ta có các tập hợp A thỏa mãn điều kiện của bài toán là:

{a; b}, {a; b; c}, {a; b; d}, {a; b; c; d}.  

Bài 7 trang 13 SBT Toán 10 Tập 1: Cho các tập hợp A = {1; 2; 3; 4; 5} và B = {1; 3; 5; 7; 9}. Hãy tìm tập hợp M có nhiều phần tử nhất thỏa mãn M ⊂ A và M ⊂ B.

Lời giải:

Do M ⊂ A nên các phần tử của tập hợp M đều là các phần tử của tập A.

Do M ⊂ B nên các phần tử của tập hợp M đều là các phần tử của tập B.

Các phần tử vừa thuộc tập A vừa thuộc tập B là 1; 3; 5.

Do đó tập hợp M có nhiều phần tử nhất thỏa mãn M ⊂ A và M ⊂ B là tập hợp các phần tử vừa thuộc A vừa thuộc B.

Vậy M = {1; 3; 5}.

Bài 8 trang 13 SBT Toán 10 Tập 1: Viết các tập hợp sau đây dưới dạng liệt kê các phần tử:

a) A = {y ∈ ℕ | y = 10 – x², x ∈ ℕ};

b) B = $\left\{x\in \mathbb{N}|\frac{6}{6-x}\in \mathbb{N}\right\}$;

c) C = {x ∈ ℕ | 2x – 3 ≥ 0 và 7 – x ≥ 2};

d) D = {(x; y) | x ∈ ℕ, y ∈ ℕ, x + 2y = 8}. 

Lời giải:

a) Do x, y đều là các số tự nhiên nên ta lần lượt thay các giá trị x bởi các số tự nhiên 0; 1; 2; ... vào y = 10 – x² để tìm các số y thỏa mãn là số tự nhiên.

Với x = 0 thì y = 10 – 0² = 10;

Với x = 1 thì y = 10 – 1² = 9;

Với x = 2 thì y = 10 – 2² = 6;

Với x = 3 thì y = 10 – 3² = 1;

Với x = 4 thì y = 10 – 4² = – 6 ∉ ℕ, ta dừng lại.

Do đó các số tự nhiên y thỏa mãn tập A là 1; 6; 9; 10.

Vậy A = {1; 6; 9; 10}.

b) Vì $\frac{6}{6-x}\in \mathbb{N}$ nên 6 phải chia hết cho (6 – x) hay (6 – x) là ước tự nhiên của 6.

Mà các ước tự nhiên của 6 là: 1, 2, 3, 6.

Với 6 – x = 1, suy ra x = 5 ∈ ℕ nên x = 5 thỏa mãn.

Với 6 – x = 2, suy ra x = 4 ∈ ℕ nên x = 4 thỏa mãn.

Với 6 – x = 3, suy ra x = 3 ∈ ℕ nên x = 3 thỏa mãn.

Với 6 – x = 6, suy ra x = 0 ∈ ℕ nên x = 0 thỏa mãn.

Vậy B = {0; 3; 4; 5}.

c) Ta có: 2x – 3 ≥ 0 ⇔ x ≥ $\frac{3}{2}$.

Và 7 – x ≥ 2 ⇔ x ≤ 7 – 2 ⇔ x ≤ 5.

Do đó, $\frac{3}{2}$≤ x ≤ 5.

Mà x ∈ ℕ và $\frac{3}{2}=1,5$ nên x là các số tự nhiên lớn hơn hoặc bằng 2 và nhỏ hơn hoặc bằng 5, đó là 2; 3; 4; 5.

Vậy C = {2; 3; 4; 5}.

d) Ta có: x + 2y = 8 ⇔ x = 8 – 2y.

Do x ∈ ℕ, y ∈ ℕ nên ta có các trường hợp sau:

+ Với y = 0 thì x = 8 – 2 . 0 = 8

+ Với y = 1 thì x = 8 – 2 . 1 = 6

+ Với y = 2 thì x = 8 – 2 . 2 = 4

+ Với y = 3 thì x = 8 – 2 . 3 = 2

+ Với y = 4 thì x = 8 – 2 . 4 = 0

+ Với y = 5 thì x = 8 – 2 . 5 = – 2 ∉ ℕ, ta dừng lại.

Do đó ta có các cặp số (x; y) thỏa mãn là: (0; 4); (2; 3); (4; 2); (6; 1); (8; 0).

Vậy D = {(0; 4); (2; 3); (4; 2); (6; 1); (8; 0)}.

Bài 9 trang 13 SBT Toán 10 Tập 1: Cho hai tập hợp A = {2k + 1 | k ∈ ℤ} và B = {6l + 3 | l ∈ ℤ}. Chứng minh rằng B ⊂ A.

Lời giải:

Để chứng minh B ⊂ A, ta chứng minh mọi phần tử của B đều là phần tử của A.

Lấy phần tử x tùy ý của B, ta có: x = 6l + 3, l ∈ ℤ.

Ta viết: x = 2 . 3l + 2 + 1 = 2(3l + 1) + 1 = 2k + 1 với k = 3l­ + 1 ∈ ℤ.

Suy ra x ∈ A.

Vậy, với mọi x ∈ B ta đều có x ∈ A. Do đó, B ⊂ A.

Bài 10 trang 13 SBT Toán 10 Tập 1: Cho hai tập hợp A = {1; 2; a} và B = {1; $a^2$}. Tìm tất cả các giá trị của a sao cho B ⊂ A.

Lời giải:

Ta có B ⊂ A khi mọi phần tử của tập B đều là phần tử của tập A.

Tập A có ba phần tử là 1; 2; a.

Tập B có hai phần tử là 1; a².

Do 1 ∈ A nên để B ⊂ A thì a² ∈ A hay a² = 1 hoặc a² = 2 hoặc a² = a.

Với a² = 1 thì a = 1 hoặc a = – 1.

Với a² = 2 thì a = $\sqrt{2}$ hoặc a = $-\sqrt{2}$.

Với a² = a ⇔ a² – a = 0 ⇔ a(a – 1) = 0 ⇔ a = 0 hoặc a = 1.

Vậy các giá trị của a để thỏa mãn yêu cầu là: $-\sqrt{2}$; – 1; 0; 1; $\sqrt{2}$.