Giải sách bài tập Toán lớp 10 Bài tập cuối chương 10

Câu 1 trang 102 SBT Toán 10 Tập 2: Một hộp có 4 viên bi xanh, 5 viên bi đỏ có kích thước và khối lượng như nhau. Lấy ra ngẫu nhiên đồng thời 2 viên bi. Xác suất của biến cố “2 viên bi lấy ra đều là bi xanh” là:

A.$\frac{1}{2}$

B.$\frac{1}{3}$

C.$\frac{1}{5}$

D.$\frac{1}{6}$

Lời giải:

Đáp án đúng là: D

Số phần tử của không gian mẫu n(Ω) = $C_9^2$  = 36

Gọi A là biến cố: “2 viên bi lấy ra đều là bi xanh”. Do đó ta chọn 2 bi xanh và 0 bi đỏ

Số phần tử của biến cố A là: n(A) = $C_4^2$  = 6

Xác suất của biến cố A là: P(A) = $\frac{6}{36}=\frac{1}{6}$ .

Câu 2 trang 102 SBT Toán 10 Tập 2: Gieo 2 con xúc xắc cân đối và đồng chất. Xác suất để tích số chấm xuất hiện bằng 7 là:

A. 0;

B. $\frac{1}{36}$ ;

C. $\frac{1}{7}$ ;

D. $\frac{1}{6}$ .

Lời giải:

Đáp án đúng là: A

Gọi A là biến cố: “Tích số chấm xuất hiện bằng 7”.

Đây là biến cố không thể nên xác suất của nó bằng 0.

Câu 3 trang 102 SBT Toán 10 Tập 2: Tung 3 đồng xu cân đối và đồng chất. Xác suất để có ít nhất một đồng xu xuất hiện mặt sấp là:

A.$\frac{1}{2}$

B.$\frac{7}{8}$

C.$\frac{1}{3}$

D.$\frac{1}{4}$

Lời giải:

Đáp án đúng là: B

Số phần tử của không gian mẫu n(Ω) = 2³ = 8.

Gọi A là biến cố: “có ít nhất một đồng xu xuất hiện mặt sấp”

Ta có biến cố đối của biến cố A là: $\overline{A}$  “Không có đồng xu nào xuất hiện mặt sấp”

$\overline{A}$ = {NNN}. Số phần tử của biến cố $\overline{A}$  là: n( $\overline{A}$) = 1

⇒ P( $\overline{A}$) = $\frac{1}{8}$

Vì vậy xác suất của biến cố A là: P(A) = $1-\frac{1}{8}=\frac{7}{8}$ .

Câu 4 trang 102 SBT Toán 10 Tập 2: Một hộp chứa 2 loại bi xanh và đỏ. Lấy ra ngẫu nhiên từ hộp 1 viên bi. Biết xác suất lấy được bi đỏ là 0,3. Xác suất lấy được bi xanh là:

A. 0,3;

B. 0,5;

C. 0,7;

D. 0,09.

Lời giải:

Đáp án đúng là: C

Vì trong hộp chỉ có bi xanh và bi đỏ nên biến cố lấy được 1 viên bi đỏ và biến cố lấy được 1 viên bi xanh là hai biến cố đối. Do đó xác xuất để lấy được bi xanh là: 1 – 0,3 = 0,7.

Câu 5 trang 102 SBT Toán 10 Tập 2: Gieo một con xúc xắc bốn mặt cân đối và đồng chất ba lần. Xác suất xảy ra biến cố “Có ít nhất một lần xuất hiện đỉnh ghi số 4” là:

A.$\frac{1}{4}$

B.$\frac{27}{64}$

C.$\frac{37}{64}$

D.$\frac{3}{4}$

Lời giải:

Đáp án đúng là: C

Số phần tử của không gian mẫu n(Ω) = 4³ = 64

Gọi A là biến cố “Có ít nhất một lần xuất hiện đỉnh ghi số 4”

Biến cố đối của biến cố A là $\overline{A}$ : “Không có lần nào xuất hiện đỉnh ghi số 4”

Vì không có lần nào xuất hiện đỉnh ghi số 4 nên mỗi lần gieo có 3 kết quả thuận lợi có thể sảy ra. Số phần tử của biến cố $\overline{A}$  là: n( $\overline{A}$) = 3³ = 27.

⇒ P( $\overline{A}$) = $\frac{27}{64}$ .

Vì vậy xác suất của biến cố A là: P(A) = $1-\frac{27}{64}=\frac{37}{64}$ .

Câu 6 trang 102 SBT Toán 10 Tập 2: Chọn ra ngẫu nhiên 2 người từ 35 người trong lớp của Hùng. Xác suất xảy ra biến cố “Hùng được chọn” là:

A.$\frac{2}{35}$

B.$\frac{1}{34}$

C.$\frac{1}{35}$

D.$\frac{1}{17}$

Lời giải:

Đáp án đúng là: A

Số phần tử của không gian mẫu n(Ω) =  $C_{35}^2$

Gọi A là biến cố: “Hùng được chọn”

Vì có bạn Hùng được chọn nên ta chọn 1 trong 34 người còn lại. Số phần tử của biến cố A là:  $C_{34}^1$

Xác xuất của biến cố A là: P(A) = $\frac{C_{34}^1}{C_{35}^2}=\frac{2}{35}$ .

Câu 7 trang 102 SBT Toán 10 Tập 2: Xếp 4 quyển sách toán và 2 quyển sách văn thành một hàng ngang trên giá sách một cách ngẫu nhiên. Xác suất xảy ra biến cố “2 quyển sách văn không được xếp cạnh nhau” là:

A.$\frac{1}{3}$

B.$\frac{2}{3}$

C.$\frac{1}{2}$

D.$\frac{1}{5}$

Lời giải:

Đáp án đúng là: B

Số phần tử của không gian mẫu là: n(Ω) = 6! = 720

Gọi A là biến cố: “2 quyển sách văn không được xếp cạnh nhau”

Biến cố đối của biến cố A là $\overline{A}$ : “2 quyển sách văn được xếp cạnh nhau”

Vì 2 quyển sách văn được xếp cạnh nhau nên ta coi 2 quyển sách văn là 1 vậy lúc này có 5 vị trí xếp và có 5! cách xếp, xếp 2 quyển sách văn có 2! cách xếp. Số phần tử của biến cố $\overline{A}$  là: n( $\overline{A}$) = 5!.2! = 240

Vì vậy xác suất của biến cố A là: P(A) = 1 – P( $\overline{A}$) = $1-\frac{240}{720}=\frac{2}{3}$ .

Câu 8 trang 102 SBT Toán 10 Tập 2:  Cô giáo chia tổ của Lan và Phương thành hai nhóm, mỗi nhóm gồm 4 người để làm việc nhóm một cách ngẫu nhiên. Xác suất của biến cố Lan và Phương thuộc cùng một nhóm là:

A.$\frac{1}{2}$

B.$\frac{1}{3}$

C.$\frac{4}{7}$

D.$\frac{3}{7}$

Lời giải:

Đáp án đúng là: D

Số phần tử của không gian mẫu: n(Ω) = $C_8^4$  = 70

Gọi A là biến cố “Lan và Phương ở cùng một nhóm”

Có 2 trường hợp xảy ra là Lan và Phương ở nhóm 1 hoặc Lan, Phương ở nhóm 2. Do đó nhóm có Lan và Phương ta chọn thêm 2 người trong 6 người

Số phần tử của biến cố A là: n(A) = $2.C_6^2$  = 30

Xác suất của biến cố A là: P(A) = $\frac{30}{70}=\frac{3}{7}$ .

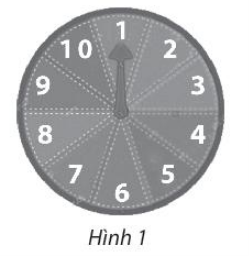
Bài 1 trang 103 SBT Toán 10 Tập 2: Trên bàn có một tấm bìa hình tròn được chia thành 10 hình quạt bằng nhau và được đánh số từ 1 đến 10 như Hình l . Cường quay mũi tên ở tâm 3 lần và quan sát xem khi mỗi lần dừng lại nó chỉ vào ô số mấy. Tính xác suất của các biến cố sau:

A: “Cả 3 lần mũi tên đều chỉ vào ô ghi số lẻ”;

B: “Tích 3 số mũi tên chỉ vào là số chia hết cho 5”.

Lời giải:

Số phần tử của không gian mẫu: n(Ω) = 10³ = 1000

A: “Cả 3 lần mũi tên đều chỉ vào ô ghi số lẻ”

Vì cả 3 lần mũi tên đều chỉ vào ô ghi số lẻ mà có 5 số lẻ là: 1; 3; 5; 7; 9

Số phần tử của biến cố A là: n(A) = 5³ = 125

Xác suất của biến cố A là: P(A) =  $\frac{125}{1000}=\frac{1}{8}$

B: “Tích 3 số mũi tên chỉ vào là số chia hết cho 5”.

Biến cố đối của biến cố B là $\overline{B}$ : “Tích 3 số mũi tên chỉ vào là số không chia hết cho 5”.

Để tích 3 số mũi tên chỉ vào không chia hết cho 5 thì cả 3 số phải không chia hết cho 5 và có 8 số không chia hết cho 5.

Số phần tử của biến cố $\overline{B}$  là: n( $\overline{B}$) = 8³ = 512

Xác suất của biến cố B là: P(B) = $1-\frac{512}{1000}=\frac{61}{125}$ .

Bài 2 trang 103 SBT Toán 10 Tập 2: Mật khẩu mở máy tính của An gồm 8 kí tự, trong đó 2 kí tự đầu là chữ số, 6 kí tự sau là các chữ cái thuộc tập hợp {A; B; C, D}. Không may An quên mất 3 kí tự đầu tiên. An chọn ra 2 chữ số và một chữ cái thuộc tập hợp trên một cách ngẫu nhiên và thử mở máy tính. Tính xác suất để An mở được máy tính.

Lời giải:

An cần 3 kí tự đầu tiên, đối với 2 chữ số đầu có: 10² (cách); đối với kí tự thứ ba có 4 (cách). Khi đó số phần tử của không gian mẫu: n(Ω) = 10.10.4 = 400.

Vì chỉ có 1 dãy số đúng để mở được máy tính nên xác xuất để An mở được máy tính là: $\frac{1}{400}$ .

Bài 3 trang 103 SBT Toán 10 Tập 2: Tổ 3 có 6 bạn là Hoà, Hiền, Hiệp, Hương, Thành và Khánh. Chọn ngẫu nhiên 2 bạn trong tổ. Hãy tính xác suất của các biến cố:

A: “Tên của hai bạn được chọn đều bắt đầu bằng chữ cái H”,

B: “Tên của ít nhất một bạn được chọn có chứa dấu huyền”,

C: “Hoà được chọn còn Hiền không được chọn”.

Lời giải:

Số phần tử của không gian mẫu: n(Ω) =  $C_6^2=15$

A: “Tên của hai bạn được chọn đều bắt đầu bằng chữ cái H”,

Ta chọn 2 bạn trong 4 bạn có tên bắt đầu bằng chữa cái H. Khi đó số phần tử của biến cố A là:  $C_4^2=6$

Xác suất của biến cố A là: P(A) = $\frac{6}{15}=\frac{2}{5}$ .

B: “Tên của ít nhất một bạn được chọn có chứa dấu huyền”

Biến cố đối của biến cố B là $\overline{B}$ : “Tên của các bạn được chọn không chứa dấu huyền”

Ta chọn 2 trong 3 bạn tên không có chứa dấu huyền. Số phần tử của biến cố $\overline{B}$  là:  $C_3^2$

Xác suất của biến cố B là: P(B) = $1-\frac{C_3^2}{C_6^2}=\frac{4}{5}$ .

C: “Hoà được chọn còn Hiền không được chọn”.

Vì Hoà được chọn mà hiền không được chọn nên ta chọn 1 bạn trong 4 bạn còn lại. số phần tử của biến cố C là: n(C) = 4

Xác xuất của biến cố C là: P(C) = $\frac{4}{15}$ .

Bài 4 trang 103 SBT Toán 10 Tập 2:  Một hộp có 5 lá thăm cùng loại được đánh số 2; 4; 6; 8; 10. Lấy ra ngẫu nhiên từ hộp 2 lá thăm. Tính xác suất của các biến cố sau:

A: “Tổng các số ghi trên hai lá thăm bằng 11”;

B: “Tích các số ghi trên hai lá thăm là số tròn chục”.

Lời giải:

Số phần tử của không gian mẫu: n(Ω) =  $C_5^2=10$

A: “Tổng các số ghi trên hai lá thăm bằng 11”

Đây là biến cố không thể nên P(A) = 0

B: “Tích các số ghi trên hai lá thăm là số tròn chục”.

Biến cố đối của biến cố B là $\overline{B}$ : “Tích các số ghi trên hai lá thăm là số không tròn chục”

Vì tích của hai số ghi trên hai lá thăm không tròn trục nên ta có hai số được chọn không có số 10, ta chọn 2 số trong 4 số. Số phần tử của biến cố $\overline{B}$  là:  $C_4^2=6$

Xác suất của biến cố B là: P(B) =  $1-\frac{6}{10}=\frac{2}{5}$

Bài 5 trang 103 SBT Toán 10 Tập 2: Doanh nghiệp A chọn ngẫu nhiên 2 tháng trong năm 2020 để tri ân khách hàng. Doanh nghiệp B cũng chọn ngẫu nhiên 1 tháng trong năm đó để tri ân khách hàng. Tính xác suất của biến cố “Hai doanh nghiệp tri ân khách hàng cùng một tháng trong năm”.

Lời giải:

Số phần tử của không gian mẫu: n(Ω) =  $C_{12}^2.C_{12}^1=792$

Gọi A là biến cố: “Hai doanh nghiệp tri ân khách hàng cùng một tháng trong năm”

Ta có doanh nghiệp A có  cách chọn và doanh nghiệp B có 2 cách chọn

Số phần tử của biến cố A là: n(A) = $2.C_{12}^2$  = 132

Xác suất của biến cố A là: P(A) = $\frac{132}{792}=\frac{1}{6}$ .

Bài 6 trang 103 SBT Toán 10 Tập 2:  Lớp học của hai bạn Hà và Giang có 32 học sinh. Cô giáo chia các bạn vào 4 tổ, mỗi tổ có 8 học sinh một cách ngẫu nhiên. Tính xác suất của các biến cố “Hà và Giang được xếp ở hai tổ khác nhau”.

Lời giải:

Số phần tử của không gian mẫu: n(Ω) =  $C_{32}^8.C_{24}^8.C_{16}^8$

Gọi A là biến cố: “Hà và Giang được xếp ở hai tổ khác nhau”

Biến cố đối của biến cố A là: $\overline{A}$  “Hà và Giang được xếp ở cùng 1 tổ”

Có 4 trường hợp xảy ra là Hà và Giang có thể ở tổ 1, tổ 2, tổ 3 hoặc tổ 4.

Mỗi trường hợp có số cách chọn là: $C_{30}^6.C_{24}^8.C_{16}^8$  (vì tổ của Hà và Giang ta chọn thêm 6 bạn trong 30 bạn, chọn 8 trong 24 bạn và 8 trong 16 bạn cuối cùng còn 8 bạn còn lại vào một tổ)

Số phần tử của biến cố $\overline{A}$  là: n( $\overline{A}$) = 4.$C_{30}^6.C_{24}^8.C_{16}^8$

Xác xuấ của biến cố A là: P(A) = $1-\frac{4.C_{30}^6.C_{24}^8.C_{16}^8}{C_{32}^8.C_{24}^8.C_{16}^8}=\frac{24}{31}$ .

Bài 7 trang 103 SBT Toán 10 Tập 2: Một hộp chứa 2 quả bóng xanh và một số quả bóng trắng. Lấy ra ngẫu nhiên 2 quả bóng từ hộp. Biết rằng xác suất chọn được 2 quả bóng khác màu là  $\frac{10}{21}$.

a) Tính xác suất 2 quả bóng lấy ra có cùng màu.

b) Hỏi trong hộp có bao nhiêu quả bóng?

Lời giải:

a) Xác xuất 2 quả bóng lấy ra có cùng màu là: $1-\frac{10}{21}=\frac{11}{21}$ .

b) Gọi k là số quả bóng trắng trong hộp (k  ℕ^*)

Số phần tử của không gian mẫu là: n(Ω) =   $C_{k+2}^2$

Vì 2 quả bóng được chọn khác màu nên ta có mỗi loại 1 quả và có xác suất là $\frac{10}{21}$

Ta có  $\frac{C_2^1.C_k^1}{C_{k+2}^2}=\frac{10}{21}$

$\iff \frac{2k}{C_{k+2}^2}=\frac{10}{21}$

$\iff 42k=10C_{k+2}^2$ 

$\iff 42k=10.\frac{(k+2)!}{2!k!}$

$\iff 42k=5.\frac{(k+2)(k+1).k!}{k!}$

$\iff$42k = 5(k + 2)(k + 1)

$\iff$5k² – 27k + 10 = 0

$\iff$ k = 5 hoặc k =  $\frac{2}{5}$

Kết hợp với điều kiện k = 5 thoả mãn

Vậy trong hộp có 7 quả bóng