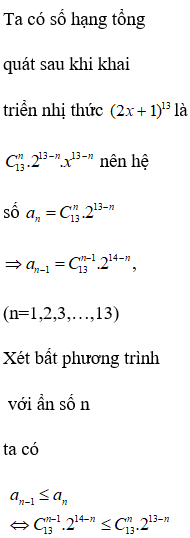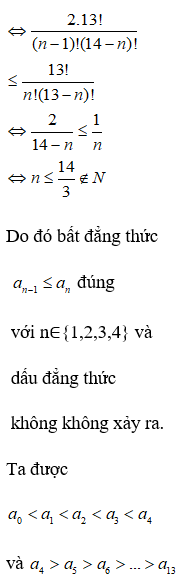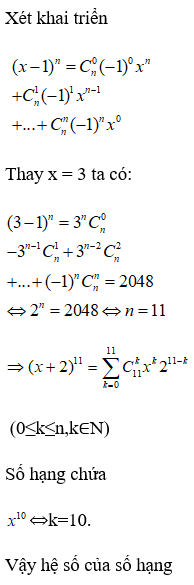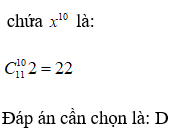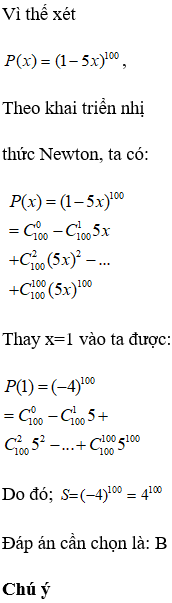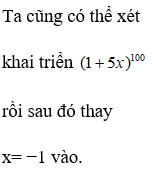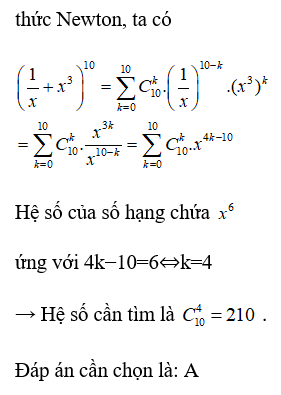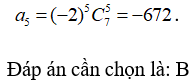15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Nhị thức newton có đáp án (Thông hiểu)

Câu 1:

Trong khai triển biểu thức $F = {(\sqrt{3} + \sqrt[3]{2})}^{9}$ số hạng nguyên có giá trị lớn nhất là

A. 8

B. 4536

C. 4528

D.4520

Xem đáp án

Ta có số hạng tổng quát

$T_{k + 1} = C_{9}^{k} (\sqrt{3})^{9 - k} (\sqrt[3]{2})^{k}$

Để $T_{k + 1}$ là một số nguyên thì

$\begin{array}{l} \{\begin{matrix} k \in N \\ 0 \leq k \leq 9 \\ (9 - k) ⋮ 2 \\ k ⋮ 3 \end{matrix} \\ \Leftrightarrow [\begin{matrix} k = 3 \Rightarrow T_{4} = C_{9}^{3} {(\sqrt{3})}^{6} {(\sqrt[3]{2})}^{3} = 4536 \\ k = 9 \Rightarrow T_{10} = C_{9}^{9} {(\sqrt{3})}^{0} {(\sqrt[3]{2})}^{9} = 8 \end{matrix} \end{array}$

Vậy trong khai triển có hai số hạng

nguyên là $T_{4} = 4536$ và $T_{10} = 8$ .

Đáp án cần chọn là: B

Câu 2:

Cho x là số thực dương. Khai triển nhị thức Newton của biểu thức ${(x^{2} + \frac{1}{2})}^{12}$ ta có hệ số của số hạng chứa $x^{m}$ bằng 495. Tìm tất cả các giá trị của tham số m.

A. m=4,m=8.

B. m=0.

C. m=0,m=12.

D. m=8.

Xem đáp án

Theo khai triển nhị thức Newton, ta có

$\begin{array}{l} {(x^{2} + \frac{1}{2})}^{12} = \sum_{k = 0}^{12} C_{12}^{k} . (x^{2})^{12 - k} . {(\frac{1}{x})}^{k} \\ = \sum_{k = 0}^{12} C_{12}^{k} . x^{24 - 2 k} . \frac{1}{x^{k}} = \sum_{k = 0}^{12} C_{12}^{k} . x^{24 - 3 k} \end{array}$

Hệ số của số hạng chứa $x^{m}$ ứng với

$\begin{array}{l} \{\begin{matrix} C_{12}^{k} = 495 \\ 24 - 3 k = m \end{matrix} \Leftrightarrow \frac{12!}{(12 - k)! . k!} = 495 \\ \Rightarrow [\begin{matrix} k = 4 \Rightarrow m = 12 \\ k = 8 \Rightarrow m = 0 \end{matrix} \end{array}$

Đáp án cần chọn là: C

Câu 3:

Tìm hệ số có giá trị lớn nhất trong khai triển đa thức $P (x) = {(2 x + 1)}^{13} = a_{0} x^{13} + a_{1} x^{12} + ... + a^{13}$

A. 366080

B. 4536

C. 4528

D. 4520

Xem đáp án

Câu 4:

Hệ số của số hạng chứa $x^{10}$ trong khai triển nhị thức ${(x + 2)}^{n}$ biết n là số nguyên dương thỏa mãn $3^{n} C_{0}^{n} - 3^{n - 1} C_{n}^{1} + 3^{n - 2} C_{n}^{2} - ... + {(- 1)}^{n} C_{n}^{n} = 2048$ là:

A. $22 x^{10}$

B. $123 x^{10}$

C. 123

D. 22

Xem đáp án

Câu 5:

Tính tổng $S = C_{100}^{0} - 5 C_{100}^{1} + 5^{2} C_{100}^{2} - ... + 5^{100} C_{100}^{100}$

A. $6^{100}$

B. $4^{100}$

C. $2^{300}$

D. $3^{200}$

Xem đáp án

Câu 6:

Hệ số của $x^{8}$ trong khai triển biểu thức $x^{2} {(1 + 2 x)}^{10} - x^{4} {(3 + x)}^{8}$ thành đa thức bằng

A. 19110

B. 7770

C. 5850

D. 11521

Xem đáp án

Câu 7:

Tìm hệ số của $x^{6}$ trong khai triển ${(\frac{1}{x} + x^{3})}^{3 n + 1}$ với x≠0, biết n là số nguyên dương thỏa mãn điều kiện $3 C_{n + 1}^{2} + n P_{2} = 4 A_{n}^{2}$ .

A. 210

B. 252

C. 120

D. 45

Xem đáp án

Câu 8:

Cho n là số dương thỏa mãn $5 C_{n}^{n - 1} = C_{n}^{3}$ . Số hạng chứa $x^{5}$ trong khai triển nhị thức Newton $P = {(\frac{n x^{2}}{14} - \frac{1}{x})}^{n}$ với x≠0 là

A. $\frac{- 35}{16}$

B. $\frac{- 16}{35}$

C. $\frac{- 35}{16} x^{5}$

D. $\frac{- 16}{35} x^{5}$

Xem đáp án

Câu 9:

Giả sử có khai triển ${(1 - 2 x)}^{n} = a_{0} + a_{1} x + a_{2} x^{2} + ... + a_{n} x^{n}$ . Tìm $a_{5}$ biết $a_{0} + a_{1} + a_{2} = 71$ .

A. $672 x^{5}$

B. -672

C. $- 672 x^{5}$

D. 672

Xem đáp án

Câu 10:

Giá trị của biểu thức $S = C_{2018}^{0} + 2 C_{2018}^{1} + 2^{2} C_{2018}^{2} + ... + 2^{2017} C_{2018}^{2017} + 2^{2018} C_{2018}^{2018}$ bằng:

A. $3^{2018}$

B. $2^{2018}$

C. $3^{2019}$

D. $2^{2019}$

Xem đáp án

Ta có:

$\begin{array}{l} (a + b)^{2018} \\ = C_{2018}^{0} a^{2018} + C_{2018}^{1} a^{2017} b + \\ C_{2018}^{2} a^{2016} b^{2} + . . . + C_{2018}^{2017} a b^{2017} + C_{2018}^{2018} b^{2018} \end{array}$

Thay a=1,b=2 ta có:

$\begin{array}{l} (1 + 2)^{2018} = C_{2018}^{0} 1^{2018} + C_{2018}^{1} 1^{2017} . 2 \\ + C_{2018}^{2} 1^{2016} . 2^{2} + . . . + C_{2018}^{2017} 1 . 2^{2017} + C_{2018}^{2018} 2^{2018} \\ \Leftrightarrow 3^{2018} = C_{2018}^{0} + 2 C_{2018}^{1} + 2^{2} C_{2018}^{2} \\ + . . . + 2^{2017} C_{2018}^{2017} + 2^{2018} C_{2018}^{2018} \end{array}$

Đáp án cần chọn là: A

Câu 11:

Đẳng thức nào sau đây sai?

A. $2^{n} = C_{n}^{0} + C_{n}^{1} + C_{n}^{2} + ... + C_{n}^{n}$

B. $0 = C_{n}^{0} - C_{n}^{1} + C_{n}^{2} - ... + {(- 1)}^{n} C_{n}^{n}$

C. $1 = C_{n}^{0} - 2 C_{n}^{1} + 4 C_{n}^{2} - ... + {(- 2)}^{n} C_{n}^{n}$

D. $3^{n} = C_{n}^{0} + 2 C_{n}^{1} + 4 C_{n}^{2} + ... + 2^{n} C_{n}^{n}$

Xem đáp án

Ta có

$(1 + x)^{n} = C_{n}^{0} + C_{n}^{1} x + C_{n}^{2} x^{2} + . . . + C_{n}^{n} x^{n}$

Cho x=1 thì A đúng.

Cho x=−1 thì B đúng.

Cho x=2 thì D đúng.

Cho x=−2 thì

$(- 1)^{n} = C_{n}^{0} - 2 C_{n}^{1} + C_{n}^{2} 2^{2} - . . . + C_{n}^{n} (- 2)^{n}$

Vậy C sai.

Đáp án cần chọn là: C

Câu 12:

Cho biểu thức $S = C_{2017}^{1009} + C_{2017}^{1010} + C_{2017}^{1011} + C_{2017}^{1012} + ... + C_{2017}^{1017}$ . Khẳng định nào sau đây đúng?

A. $S = 2^{2017} - 2$

B. $S = 2^{2016}$

C. $S = 2^{2015}$

D. $S = 2^{2014}$

Xem đáp án

Áp dụng tính chất $C_{n}^{k} = C_{n}^{n - k}$ ta có:

$\begin{array}{l} S = C_{2017}^{1009} + C_{2017}^{1010} + C_{2017}^{1011} + C_{2017}^{1012} + . . . + C_{2017}^{1017} \\ = C_{2017}^{1008} + C_{2017}^{1007} + C_{2017}^{1006} + C_{2017}^{1005} + . . . + C_{2017}^{0} \end{array}$

Suy ra:

$\begin{array}{l} 2 S = C_{2017}^{0} + . . . + C_{2017}^{1005} + C_{2017}^{1006} + C_{2017}^{1007} + C_{2017}^{1008} \\ + C_{2017}^{1009} + C_{2017}^{1010} + C_{2017}^{1011} + C_{2017}^{1012} + . . . + C_{2017}^{1017} \end{array}$

Ta có:

$\begin{array}{l} (a + b)^{2017} = C_{2017}^{0} a^{2017} + C_{2017}^{1} a^{2016} b + \\ C_{2017}^{2} a^{2015} b^{2} + . . . + C_{2017}^{2016} a b^{2016} + C_{2017}^{2017} b^{2017} \end{array}$

Thay a=1,b=1 ta có:

$\begin{array}{l} 2^{2017} = C_{2017}^{0} + C_{2017}^{1} + C_{2017}^{2} \\ + . . . + C_{2017}^{2016} + C_{2017}^{2017} \\ \Leftrightarrow 2^{2017} = 2 S \Leftrightarrow S = 2^{2016} \end{array}$

Đáp án cần chọn là: B

Câu 13:

Tổng các hệ số của tất cả các số hạng trong khai triển nhị thức ${(x - 2 y)}^{2020}$ là:

A. 2021

B. 2020

C. -1

D. 1

Xem đáp án

Theo khai triển nhị thức

Newton ta có:

$\begin{array}{l} (x - 2 y)^{2020} \\ = \sum_{k = 0}^{2020} C_{2020}^{k} x^{2020 - k} . {(- 2 y)}^{k} = \sum_{k = 0}^{2020} C_{2020}^{k} . x^{2020 - k} . {(- 2)}^{k} . y^{k} \end{array}$

Tổng các hệ số trong khai triển là:

$S = \sum_{k = 0}^{2020} C_{2020}^{k} . {(- 2)}^{k}$

Thay x=1; y=1 ta có:

$(1 - 2.1)^{2020} = (- 1)^{2020} = 1$

Vậy tổng các hệ số của tất cả các số hạng

trong khai triển nhị thức $(x - 2 y)^{2020}$ bằng 1

Đáp án cần chọn là: D

Câu 14:

Cho $S = C_{15}^{8} + C_{15}^{9} + C_{15}^{10} + ... + C_{15}^{15}$ . Tính S.

A. $2^{15}$

B. $2^{14}$

C. $2^{13}$

D. $2^{12}$

Xem đáp án

Sử dụng đẳng thức $C_{n}^{k} = C_{n}^{n - k}$

ta được:

$\begin{array}{l} S = C_{15}^{8} + C_{15}^{9} + C_{15}^{10} + . . . + C_{15}^{15} \\ = C_{15}^{7} + C_{15}^{6} + C_{15}^{5} + . . . + C_{15}^{0} \\ \Rightarrow 2 S = (C_{15}^{8} + C_{15}^{9} + C_{15}^{10} + . . . + C_{15}^{15}) \\ + (C_{15}^{7} + C_{15}^{6} + C_{15}^{5} + . . . + C_{15}^{0}) = \sum_{k = 0}^{15} C_{15}^{k} = 2^{15} \\ \Rightarrow S = 2^{14} \end{array}$

Vậy

$S = (C_{15}^{8} + C_{15}^{9} + C_{15}^{10} + . . . + C_{15}^{15}) = 2^{14}$

Đáp án cần chọn là: B

Câu 15:

Cho biểu thức $S = C_{n}^{2} + C_{n}^{3} + C_{n}^{4} + C_{n}^{5} + ... + C_{n}^{n - 2}$ . Khẳng định nào sau đây đúng?

A. $S = 2^{n} - 2 n + 2$

B. $S = 2^{n} - 2$

C. $S = 2^{n} - 2 n - 2$

D. $S = 2^{n} + n - 1$

Xem đáp án

Ta có:

$\begin{array}{l} (a + b)^{n} = C_{n}^{0} a^{n} + C_{n}^{1} a^{n - 1} b + C_{n}^{2} a^{n - 2} b^{2} \\ + . . . + C_{n}^{n - 1} a b^{n - 1} + C_{n}^{n} b^{n} \end{array}$

Thay a=1, b=1 ta có:

$\begin{array}{l} 2^{n} = C_{n}^{0} + C_{n}^{1} + . . . + C_{n}^{n - 1} + C_{n}^{n} \\ \Leftrightarrow 2^{n} = 1 + n + C_{n}^{2} + C_{n}^{3} + C_{n}^{4} \\ + C_{n}^{5} + . . . + C_{n}^{n - 2} + n + 1 \\ \Leftrightarrow 2^{n} - 2 n - 2 = C_{n}^{2} + C_{n}^{3} \\ + C_{n}^{4} + C_{n}^{5} + . . . + C_{n}^{n - 2} \end{array}$

Đáp án cần chọn là C

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Nhị thức newton có đáp án

Trắc nghiệm Nhị thức newton có đáp án (Thông hiểu)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương