10 câu hỏi trắc nghiệm thuộc Đề số 2. Top 10 Đề kiểm tra Giữa kì 1 Toán 8 (có đáp án)

Top 10 Đề kiểm tra Giữa kì 1 Toán 8 (có đáp án)

Đề số 2. Top 10 Đề kiểm tra Giữa kì 1 Toán 8 (có đáp án)

4015 lượt thi
10 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Tích của đơn thức: $x^{2}$ và đa thức $5 x^{3} - x - 1$ là :

A. $5 x^{6} - x^{3} - x^{2}$

B. $- 5 x^{5} + x^{3} + x^{2}$

C. $5 x^{5} - x^{3} - x^{2}$

D. $5 x^{5} - x - 1$

Xem đáp án

Chọn C

Câu 2:

Đa thức

3 x^{2} - 12

được phân tích thành nhân tử là :

A. $3 x {(x - 2)}^{2}$

B. $3 x (x^{2} + 4)$

C. $3 (x - 2) (x + 2)$

D. $x (3 x - 2) (3 x + 2)$

Xem đáp án

Chọn C

Câu 3:

Cho tứ giác ABCD biết $\hat{A} = 50 °; \hat{C} = 60 °; \hat{D} = 100 °$ , khi đó số đo là

A. $150 ° .$

B. $105 ° .$

C. $75 ° .$

D. $30 ° .$

Xem đáp án

Chọn A

Câu 4:

Đa thức $x^{4} - 3 x^{3} + 6 x^{2} - 7 x + m$ chia hết cho đa thức $x - 1$ khi m bằng.

A. 0.

B. $- 3$

C. 3.

D. 1.

Xem đáp án

Chọn C

Câu 5:

Giá trị nhỏ nhất của đa thức $A = x^{2} + 4 x + 11$ là

A. 7.

B. $- 2$

C. $- 4$

D. 11.

Xem đáp án

Chọn A

Câu 6:

Cho tam giác ABC vuông tại A, O là trung điểm của BC. D là điểm đối xứng với A qua O. Đẳng thức nào sai trong các đẳng thức sau?

A. $B O = \frac{1}{2} A D .$

B. $B O = \frac{1}{2} A C$

C. $A B = C D .$

D. $A D = B C .$

Xem đáp án

Chọn B

Câu 7:

1) Tìm x biết

x (x - 1) + x - 1 = 0.

2) Tính giá trị biểu thức: A =

(x - y) (x^{2} + x y + y^{2}) + 2 y^{3}

tại

x = \frac{2}{3}

và

y = \frac{1}{3}

Xem đáp án

$\begin{array}{l} x (x - 1) + (x - 1) = 0 \end{array} (x - 1) (x + 1) = 0$

$\Rightarrow x = 1$ hoặc $x = - 1.$

Vậy $x \in \{- 1; 1\} .$

2. $A = (x - y) (x^{2} + x y + y^{2}) + 2 y^{3}$

Tại

x = \frac{2}{3}

và

y = \frac{1}{3}

biểu thức A có giá trị là

A = \frac{1}{3}

Câu 8:

Cho đa thức

A = 2 x^{4} + 3 x^{3} - 4 x^{2} - 3 x + 2

và đa thức

B = x + 2

1) Làm tính chia đa thức A cho đa thức B.
2) Hãy phân tích đa thức thương của phép chia đa thức A cho đa thức B thành nhân tử.

Xem đáp án

1. Thực hiện được đúng phép chia

(2 x^{4} + 3 x^{3} - 4 x^{2} - 3 x + 2) : (x + 2) = 2 x^{3} - x^{2} - 2 x + 1

\begin{array}{l} 2 x^{3} - x^{2} - 2 x + 1 = 2 x (x^{2} - 1) - (x^{2} - 1) = (x^{2} - 1) (2 x - 1) \\ = (x - 1) (x + 1) (2 x - 1) . \end{array}

Câu 9:

Cho hình bình hành ABCD trong đó có $BC = 2AB.$ Gọi M là trung điểm của BC, N là trung điểm của AD .

1) Chứng minh rằng tứ giác MNDC là hình bình hành.

2) Kẻ DE vuông góc với AB tại E, DE cắt MN tại F. Chứng minh F là trung điểm của DE.

3) Chứng minh rằng: $\hat{A B C} = 2 \hat{B E M}$ .

Xem đáp án

Cho hình bình hành ABCD trong đó có Gọi M là trung điểm của BC, N là trung điểm của AD . 1) Chứng minh rằng tứ giác MNDC là hình bình hành. 2) Kẻ DE vuông góc với AB tại E, DE cắt MN tại F. Chứng minh F là trung điểm của DE. 3) Chứng minh rằng: . (ảnh 1)

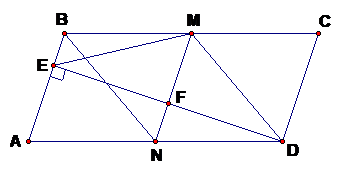
1. Chỉ ra được MC // ND và MC = ND
Do đó tứ giác MNDC là hình bình hành.

- Chỉ ra được

N F // A E

và N là trung điểm cạnh AD của tam giác DAE

\Rightarrow

F là trung điểm của DE.

Ta có:

\hat{B E M} = \hat{EMN}

(cặp góc so le trong)
Chỉ ra được tam giác MED cân tại M

\Rightarrow \hat{E M N} = \hat{N M D}

Chỉ ra được

\hat{N M D} = \hat{M N B}

Do đó

\hat{B E M} = \hat{MNB}

Mặt khác

\hat{N B M} = \hat{MNB}

(tam giác BMN cân tại M)
và

\hat{N B A} = \hat{MNB}

(cặp góc so le trong)
Vậy

\hat{A B C} = 2 \hat{B E M}

Câu 10:

Cho các số x, y, z thỏa mãn đồng thời: $x + y + z = 1; x^{2} + y^{2} + z^{2} = 1;$ $ x^{3} + y^{3} + z^{3} = 1$ . Tính giá trị của biểu thức: $M = x^{8} + y^{11} + z^{2018}$

Xem đáp án

Ta có:

(x + y + z) = x + y + z + 3 (x + y) (y + z) (z + x)

kết hợp các điều kiện đã cho ta có:

\begin{array}{l} (x + y) (y + z) (z + x) = 0 \end{array}

\Rightarrow

Một trong các thừa số của tích

(x + y) (y + z) (z + x)

phải bằng 0
Giả sử

(x + y) = 0,

kết hợp với đ/k:

x + y + z = 1 \Rightarrow z = 1

kết hợp với điều kiện:

x + y + z = 1 \Rightarrow x = y = 0.

Vậy trong 3 số

x, y, z

phải có 2 số bằng 0 và 1 số bằng 1.
Vậy

S = 1.

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Top 10 Đề kiểm tra Giữa kì 1 Toán 8 (có đáp án)

Đề số 2. Top 10 Đề kiểm tra Giữa kì 1 Toán 8 (có đáp án)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương