Đề kiểm tra 45 phút Toán 8 Chương 3 Hình Học có đáp án (Đề 4)
-
2076 lượt thi
-
8 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Phần trắc nghiệm (3 điểm)
Gọi M là điểm nằm trên đoạn tẳng AB sao cho . Tỉ số là:
Xem đáp án
Chọn B
Câu 3:
Chọn đúng (Đ), sai (S) điền vào chỗ chấm.
a) Nếu hai tam giác cân có các góc ở đỉnh bằng nhau thì đồng dạng với nhau. ...
b) Nếu với tỉ số đồng dạng là 1/2 vàvới tỉ số đồng dạng là 4/3 thì với tỉ số đồng dạng là 2/3 ....
c) Trên cạnh AB, AC của ΔABC lấy 2 điểm I và K sao cho
d) Hai tam giác đồng dạng thì bằng nhau....
Xem đáp án
a) Đ b)S c) Đ d) S
Câu 4:
Cho tam giác ABC có các cạnh và AD là đường phân giác. Tỉ số diện tích của ΔABD và diện tích của ΔACD bằng:
Xem đáp án
Chọn A
Câu 6:
Phần tự luận (7 điểm)
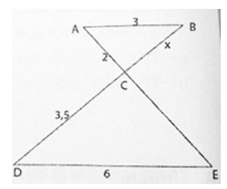
Cho tam giác ABC (AB < AC), tia phân giác của góc A cắt BC ở K. Qua trung điểm M của BC kẻ một tia song song với AK cắt đường thẳng AB ở D, cắt AC ở E. Chứng minh BD = CE
Xem đáp án
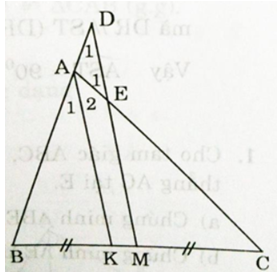
Ta có:
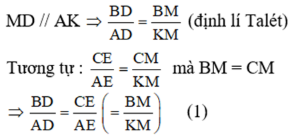
Mặt khác : ∠D1 = ∠A1 (đồng vị)
∠E1 = ∠A2 (so le trong)
∠A1 = ∠A2 (gt)
⇒ ∠D1 = ∠E1
Do đó ΔADE cân tại A ⇒ AD = AE (2)
Từ (1) và (2) ⇒ BD = CE
Câu 7:
Cho ΔABC ∼ ΔMNP theo tỉ số k = 1/2 . Tính biết
Xem đáp án
Do tỉ số diện tích bằng bình phương tỉ số đồng dạng nên ta có:
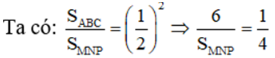
Câu 8:
Cho hình chữ nhật ABCD, kẻ AH vuông góc với đường chéo BD
a) Chứng minh ΔAHD và ΔDCB đồng dạng và
b) Gọi S là trung điểm của BH, R là trung điểm của AH.
Chứng minh SH.BD = SR.DC
c) Gọi T là trung điểm của DC. Chứng minh tứ giác DRST là hình bình hành
d) Tính góc AST
Xem đáp án
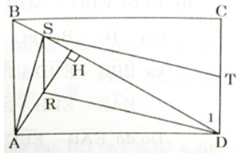
a) Hai tam giác vuông AHD và BDC có ∠ADH = ∠CBD (SLT)
⇒ ΔAHD ∼ ΔDCB (g.g)
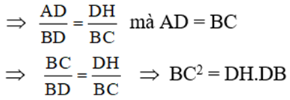
b) Ta có S, R là trung điểm của HB và AH nên SR là đường trung bình của ΔABH ⇒ SR // AB
⇒ ∠HSR = ∠HBA (đồng vị)
Mà ∠HBA = ∠D1
⇒ HSR = ∠D1
Do đó ΔSHR ∼ ΔDCB (g.g)
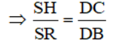
c) Ta có SR // AB và SR = AB/2 (cmt), TD = CD/2
mà AB = CD và AB // CD (gt)
⇒ SR // DT và SR = DT
Do đó Tứ giác DRST là hình bình hành
d) Ta có SR // AB mà AB ⊥ AD (gt) ⇒ SR ⊥ AD, lại có AH ⊥ SD (gt)
⇒ R là trực tâm của ΔSAD ⇒ DR là đường cao thứ ba nên DR ⊥ SA
Mà DR // ST (DRST là hình bình hành) ⇒ ST ⊥ SA
Vậy ∠AST = 90o