10 câu hỏi trắc nghiệm thuộc Trắc nghiệm Phương trình chứa ẩn ở mẫu có đáp án (Vận dụng)

Câu 1:

Cho phương trình $\frac{1}{x - 1} - \frac{7}{x - 2} = \frac{1}{(x - 1) (2 - x)}$

Bạn Long giải phương trình như sau:

Bước 1: ĐKXĐ: x ≠ 1; x ≠ 2

Bước 2: $\frac{1}{x - 1} - \frac{7}{x - 2} = \frac{1}{(x - 1) (2 - x)}$

$\Leftrightarrow \frac{x - 2}{(x - 1) (x - 2)} - \frac{7 (x - 1)}{(x - 1) (x - 2)} = \frac{1}{(x - 1) (x - 2)}$

Bước 3: $\Rightarrow$ x – 2 – 7x + 7 = 1 $\Leftrightarrow$ -6x = -4 $\Leftrightarrow$ x = $\frac{2}{3}$ (TM)

Vậy tập nghiệm của phương trình là S = { $\frac{2}{3}$ }

Chọn câu đúng.

A. Bạn Long giải sai từ bước 1

B. Bạn Long giải sai từ bước 2

C. Bạn Long giải sai từ bước 3

D. Bạn Long giải đúng

Xem đáp án

Đáp án cần chọn là: B

ĐKXĐ: x ≠ 1; x ≠ 2

Ta có $\frac{1}{x - 1} - \frac{7}{x - 2} = \frac{1}{(x - 1) (2 - x)}$

$\Leftrightarrow \frac{x - 2}{(x - 1) (x - 2)} - \frac{7 (x - 1)}{(x - 1) (x - 2)} = \frac{- 1}{(x - 1) (x - 2)}$

$\Leftrightarrow$ x – 2 – 7x + 7 = -1 $\Leftrightarrow$ -6x = -6 $\Leftrightarrow$ x = 1 (không thỏa mãn ĐK)

Vậy phương trình vô nghiệm

Bạn Long sai ở bước 2 do không đổi dấu tử số 1 khi đổi dấu mẫu

Câu 2:

Cho phương trình $\frac{1}{x - 1} - \frac{7}{x - 2} = \frac{1}{(x - 1) (2 - x)}$ .

Bạn Long giải phương trình như sau:

Bước 1: ĐKXĐ: x ≠ 1; x ≠ 2

Bước 2: $\frac{1}{x - 1} - \frac{7}{x - 2} = \frac{1}{(x - 1) (2 - x)}$

$\Leftrightarrow \frac{x - 2}{(x - 1) (x - 2)} - \frac{7 (x - 1)}{(x - 1) (x - 2)} = \frac{- 1}{(x - 1) (x - 2)}$

Bước 3: $\Rightarrow$ x – 2 – 7x + 7 = -1 $\Leftrightarrow$ -6x = -6 $\Leftrightarrow$ x = 1

Vậy tập nghiệm của phương trình là S = {1}

Chọn câu đúng.

A. Bạn Long giải sai từ bước 1

B. Bạn Long giải sai từ bước 2

C. Bạn Long giải sai từ bước 3

D. Bạn Long giải đúng

Xem đáp án

Đáp án cần chọn là: C

ĐKXĐ: x ≠ 1; x ≠ 2

Ta có $\frac{1}{x - 1} - \frac{7}{x - 2} = \frac{1}{(x - 1) (2 - x)}$

$\Leftrightarrow \frac{x - 2}{(x - 1) (x - 2)} - \frac{7 (x - 1)}{(x - 1) (x - 2)} = \frac{- 1}{(x - 1) (x - 2)}$

$\Rightarrow$ x – 2 – 7x + 7 = -1 $\Leftrightarrow$ -6x = -6 $\Leftrightarrow$ x = 1 (không thỏa mãn ĐK)

Vậy phương trình vô nghiệm

Bạn Long sai ở bước 3 do không đối chiếu với điều kiện ban đầu

Câu 3:

Cho hai biểu thức: A = 1 + $\frac{1}{2 + x}$ và B = $\frac{12}{x^{3} + 8}$ . Tìm x sao cho A = B

A. x = 0

B. x =1

C. x = -1

D. Cả A và B

Xem đáp án

Đáp án cần chọn là: D

Câu 4:

Cho hai biểu thức: A = 1 - $\frac{1}{2 - x}$ và B = $\frac{12}{x^{3} - 8}$ . Giá trị của x để A = B là

A. x = 0

B. x = 1

C. Không có x

D. x = 2

Xem đáp án

Đáp án cần chọn là: C

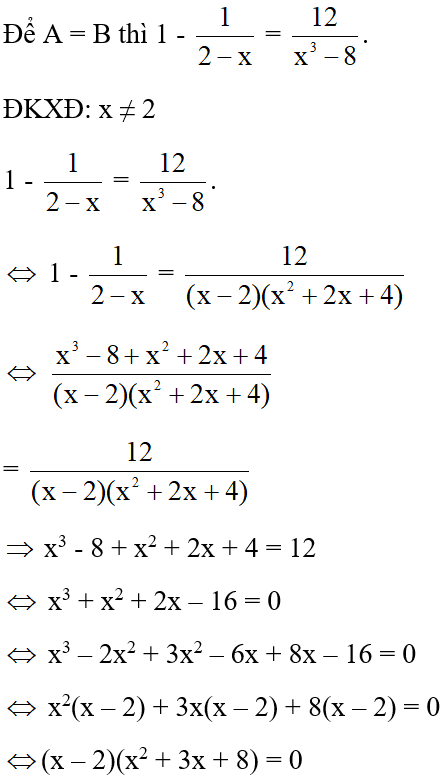
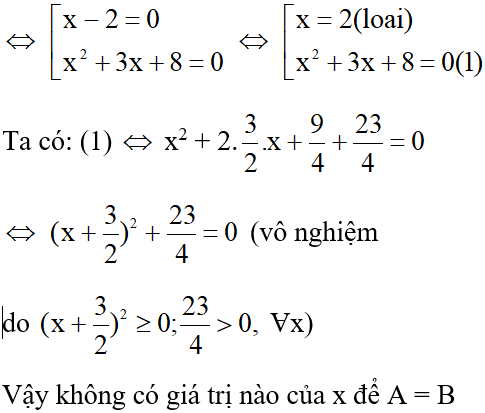
Câu 5:

Cho phương trình (1): $\frac{1}{x} + \frac{2}{x - 2} = 0$ và phương trình (2): $\frac{x - 1}{x + 2} - \frac{x}{x - 2} = \frac{5 x - 2}{4 - x^{2}}$

Khẳng định nào sau đây là đúng

A. Hai phương trình có cùng điều kiện xác định

B. Hai phương trình có cùng số nghiệm

C. Phương trình (2) có nhiều nghiệm hơn phương trình (1)

D. Hai phương trình tương đương

Xem đáp án

Đáp án cần chọn là: C

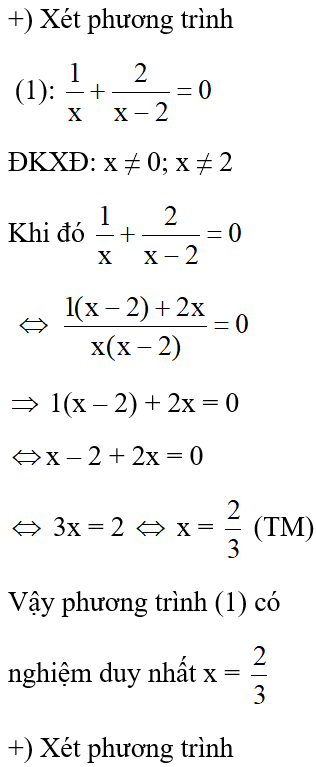
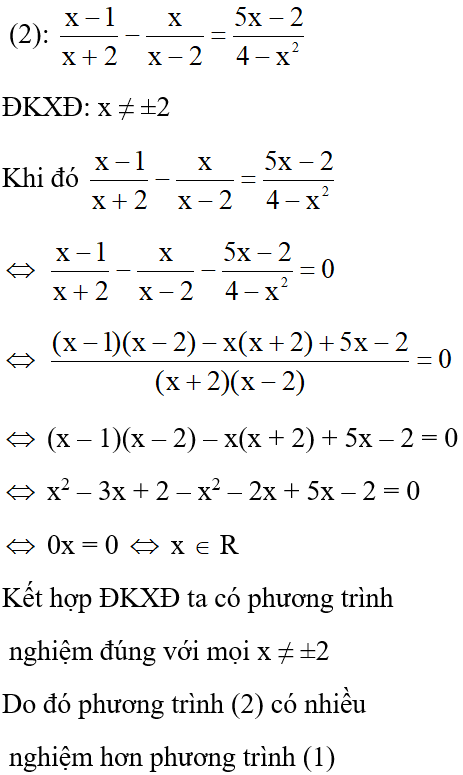
Câu 6:

Cho phương trình (1): $\frac{1}{x} + \frac{2}{x - 2} = 0$ và phương trình (2): $\frac{x - 1}{x^{2} - x} + \frac{2 x - 2}{x^{2} - 3 x + 2} = 0$ . Khẳng định nào sau đây là sai.

A. Hai phương trình có cùng điều kiện xác định

B. Hai phương trình có cùng số nghiệm

C. Hai phương trình có cùng tập nghiệm

D. Hai phương trình tương đương

Xem đáp án

Đáp án cần chọn là: A

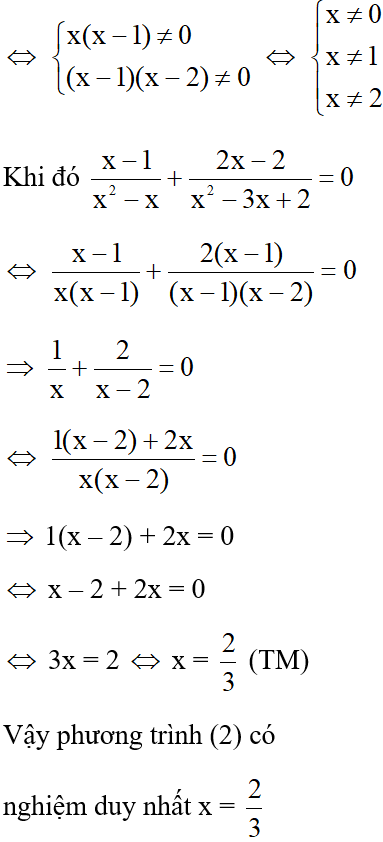
Câu 7:

Biết x₀ là nghiệm nhỏ nhất của phương trình

$\frac{1}{x^{2} + 4 x + 3} + \frac{1}{x^{2} + 8 x + 15} + \frac{1}{x^{2} + 12 x + 35} + \frac{1}{x^{2} + 16 x + 63} = \frac{1}{5}$

Chọn khẳng định đúng.

A. x₀ > 0

B. x₀ < -5B. x₀ < -5

C. x₀ = -10

D. x₀ > 5

Xem đáp án

Đáp án cần chọn là: B

Phân tích các mẫu thành nhân tử sau đó nhân cả 2 vế của phương trình với 2 ta được:

Pt $\Leftrightarrow \frac{1}{(x + 1) (x + 3)} + \frac{1}{(x + 3) (x + 5)} + \frac{1}{(x + 5) (x + 7)} + \frac{1}{(x + 7) (x + 9)} = \frac{1}{5}$

$\Leftrightarrow \frac{2}{(x + 1) (x + 3)} + \frac{2}{(x + 3) (x + 5)} + \frac{2}{(x + 5) (x + 7)} + \frac{2}{(x + 7) (x + 9)} = \frac{2}{5}$

ĐKXĐ: x ≠ {-1; -3; -5; -7; -9}

Khi đó:

Pt $\Leftrightarrow \frac{1}{x + 1} - \frac{1}{x + 3} + \frac{1}{x + 3} - \frac{1}{x + 5} + \frac{1}{x + 5} - \frac{1}{x + 7} + \frac{1}{x + 7} - \frac{1}{x + 9} = \frac{2}{5}$

$\Leftrightarrow \frac{1}{x + 1} - \frac{1}{x + 9} = \frac{2}{5}$

$\Leftrightarrow \frac{1 (x + 9) - 1 (x + 1)}{(x + 1) (x + 9)} = \frac{2 (x + 1) (x + 9)}{5 (x + 1) (x + 9)}$

$\Rightarrow$ 5[x + 9 – (x + 1)] = 2(x + 1)(x + 9)

$\Leftrightarrow$ 5(x + 9 – x – 1) = 2x² + 20x + 18

$\Leftrightarrow$ 2x² + 20x – 22 = 0

$\Leftrightarrow$ x² + 10x – 11 = 0

$\Leftrightarrow$ x² – x + 11x – 11 = 0

$\Leftrightarrow$ (x – 1)(x + 11) = 0

$\Leftrightarrow [\begin{array}{l} x - 1 = 0 \\ x + 11 = 0 \end{array}$ $\Leftrightarrow [\begin{array}{l} x = 1 \\ x = - 11 \end{array}$ (tm)

$\Rightarrow$ S = {1; -11}

Vậy x₀ = -11 < -5

Câu 8:

Cho phương trình: $\frac{1}{x^{2} + 3 x + 2} + \frac{1}{x^{2} + 5 x + 6} + \frac{1}{x^{2} + 7 x + 12} + \frac{1}{x^{2} + 9 x + 20} = \frac{1}{3}$

Tổng bình phương các nghiệm của phương trình trên là:

A. -48

B. 48

C. -50

D. 50

Xem đáp án

Đáp án cần chọn là: D

Ta có x² + 3x + 2 = (x + 1)(x + 2)

x² + 5x + 6 = (x + 2)(x + 3)

x² + 7x + 12 = (x + 3)(x + 4)

x² + 9x + 20 = (x + 4)(x + 5)

Khi đó

Pt $\Leftrightarrow \frac{1}{(x + 1) (x + 2)} + \frac{1}{(x + 2) (x + 3)} + \frac{1}{(x + 3) (x + 4)} + \frac{1}{(x + 4) (x + 5)} = \frac{1}{3}$

ĐKXĐ: x ≠ {-1; -2; -3; -4; -5}

Khi đó:

Pt $\Leftrightarrow \frac{1}{x + 1} - \frac{1}{x + 2} + \frac{1}{x + 2} - \frac{1}{x + 3} + \frac{1}{x + 3} - \frac{1}{x + 4} + \frac{1}{x + 4} - \frac{1}{x + 5} = \frac{1}{3}$

$\Leftrightarrow \frac{1}{x + 1} - \frac{1}{x + 5} = \frac{1}{3}$

$\Leftrightarrow \frac{1 (x + 5) - 1 (x + 1)}{(x + 1) (x + 5)} = \frac{(x + 1) (x + 5)}{3 (x + 1) (x + 5)}$

$\Rightarrow$ 3[x + 5 – (x + 1)] = (x + 1)(x + 5)

$\Leftrightarrow$ 3(x + 5 – x – 1) = x² + 6x + 5

$\Leftrightarrow$ x² + 6x – 7 = 0

$\Leftrightarrow$ (x – 1)(x + 7) = 0

$\Leftrightarrow [\begin{array}{l} x - 1 = 0 \\ x + 7 = 0 \end{array}$ $\Leftrightarrow [\begin{array}{l} x = 1 \\ x = - 7 \end{array}$ (tm)

$\Rightarrow$ S = {1; -7} nên tổng bình phương các nghiệm là: 1² + (-7)² = 50

Câu 9:

Số nghiệm của phương trình $\frac{x^{2} + 3 x + 2}{x + 3} - \frac{x^{2} + 2 x + 1}{x - 1} = \frac{4 x + 4}{x^{2} + 2 x - 3}$ là

A. 2

B. 1

C. 4

D. 3

Xem đáp án

Đáp án cần chọn là: B

Ta có $\frac{x^{2} + 3 x + 2}{x + 3} - \frac{x^{2} + 2 x + 1}{x - 1} = \frac{4 x + 4}{x^{2} + 2 x - 3}$

$\Leftrightarrow \frac{x^{2} + 2 x + x + 2}{x + 3} - \frac{{(x + 1)}^{2}}{x - 1} = \frac{4 (x + 1)}{x^{2} - x + 3 x - 3}$

$\Leftrightarrow \frac{(x + 2) (x + 1)}{x + 3} - \frac{{(x + 1)}^{2}}{x - 1} = \frac{4 (x + 1)}{(x + 3) (x - 1)}$

ĐK: x ≠ {1; -3}

Khi đó

Pt $\Leftrightarrow \frac{(x + 2) (x + 1) (x - 1) - {(x + 1)}^{2} (x + 3)}{(x + 3) (x - 1)} = \frac{4 (x + 1)}{(x + 3) (x - 1)}$

$\Rightarrow$ (x + 2)(x + 1)(x – 1) – (x + 1)²(x + 3) – 4(x + 1) = 0

$\Leftrightarrow$ (x + 1)[(x + 2)(x – 1) – (x + 1)(x + 3) – 4] = 0

$\Leftrightarrow$ (x + 1)(x² + x – 2 – x² – 4x – 3 – 4) = 0

$\Leftrightarrow$ (x + 1)(-3x – 9) = 0

$\Leftrightarrow [\begin{array}{l} x + 1 = 0 \\ - 3 x - 9 = 0 \end{array}$ $\Leftrightarrow [\begin{array}{l} x = - 1 (T M) \\ x = - 3 (K T M) \end{array}$

Vậy phương trình có nghiệm duy nhất x = -1

Câu 10:

Số nghiệm của phương trình $\Leftrightarrow \frac{2 x^{2} - x - 3}{(2 x - 3) (x^{2} + x + 1)} - \frac{2 x^{2} - 5 x + 3}{(2 x - 3) (x^{2} - x + 1)} = \frac{6 x - 9}{x (2 x - 3) (x^{4} + x^{2} + 1)}$

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Đáp án cần chọn là: A

ĐK: $\{\begin{cases} (2 x - 3) (x^{2} + x + 1) \neq 0 \\ (2 x - 3) (x^{2} - x + 1) \neq 0 \\ x (2 x - 3) (x^{4} + x^{2} + 1) \neq 0 \end{cases}$ (*)

Ta có: x² + x + 1 = x² + 2. $\frac{1}{2}$ .x + $\frac{1}{4} + \frac{3}{4}$ = ${(x + \frac{1}{2})}^{2} + \frac{3}{4} > 0$

x² – x + 1 = x² - 2. $\frac{1}{2}$ .x + $\frac{1}{4} + \frac{3}{4}$ = ${(x - \frac{1}{2})}^{2} + \frac{3}{4} > 0$

x⁴ + x² + 1 > 0

Do đó (*) $\Leftrightarrow \{\begin{cases} x \neq \frac{3}{2} \\ x \neq 0 \end{cases}$

Khi đó,

Pt $\Leftrightarrow \frac{(2 x - 3) (x + 1)}{(2 x - 3) (x^{2} + x + 1)} - \frac{(2 x - 3) (x - 1)}{(2 x - 3) (x^{2} - x + 1)} = \frac{3 (2 x - 3)}{x (2 x - 3) (x^{4} + x^{2} + 1)}$

$\Rightarrow$ $\frac{x + 1}{x^{2} + x + 1} - \frac{x - 1}{x^{2} - x + 1} = \frac{3}{x (x^{4} + x^{2} + 1)}$

$\Leftrightarrow \frac{(x + 1) (x^{2} - x + 1)}{(x^{2} + x + 1) (x^{2} - x + 1)} - \frac{(x - 1) (x^{2} + x + 1)}{(x^{2} - x + 1) (x^{2} + x + 1)} = \frac{3}{x (x^{4} + x^{2} + 1)}$

$\Leftrightarrow \frac{x^{3} + 1}{{(x^{2} + 1)}^{2} - x^{2}} - \frac{x^{3} - 1}{{(x^{2} + 1)}^{2} - x^{2}} = \frac{3}{x (x^{4} + x^{2} + 1)}$

$\Leftrightarrow \frac{x^{3} + 1 - x^{3} + 1}{x^{4} + x^{2} + 1} = \frac{3}{x (x^{4} + x^{2} + 1)}$

$\Leftrightarrow \frac{2}{x^{4} + x^{2} + 1} = \frac{3}{x (x^{4} + x^{2} + 1)}$

$\Leftrightarrow \frac{2 x}{x (x^{4} + x^{2} + 1)} = \frac{3}{x (x^{4} + x^{2} + 1)}$

$\Rightarrow$ 2x = 3 $\Leftrightarrow$ x = $\frac{3}{2}$ (loại)

Vậy phương trình đã cho vô nghiệm.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Phương trình chứa ẩn ở mẫu có đáp án

Trắc nghiệm Phương trình chứa ẩn ở mẫu có đáp án (Vận dụng)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương