(2023) Đề thi thử Vật Lí THPT Kim Sơn A - Ninh Bình có đáp án
(2023) Đề thi thử Vật Lí THPT Kim Sơn A - Ninh Bình có đáp án
-
137 lượt thi
-
40 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 2:
Phát biểu nào sau đây là đúng khi nói về vật dao động điều hòa?
 Xem đáp án
Xem đáp án
\(F = - kx\). Chọn A
Câu 3:
Hiện nay, hệ thống điện lưới quốc gia ở Việt Nam thường dùng dòng điện xoay chiều có tần số là:
 Xem đáp án
Xem đáp án
Chọn C
Câu 4:
Chọn câu trả lời sai?
 Xem đáp án
Xem đáp án
Tần số của dao động cưỡng bức luôn bằng tần số của ngoại lực. Chọn C
Câu 5:
Khách hàng khi vào siêu thị Go Ninh Bình. Khi đi gần tới cửa ra vào thì cửa tự động mở. Khi vào khỏi cửa thì cửa lại tự động đóng lại. Thiết bị đóng mở cửa này hoạt động dựa trên hiên tượng vật lí nào?

 Xem đáp án
Xem đáp án
Chọn B
Câu 6:
Một mạch điện xoay chiều gồm R, L, C nối tiếp nhau. Khi mắc vào hai đầu mạch điện một điện áp xoay chiều u = U0cos(ωt + π/3) V thì điện áp giữa hai bản tụ là uC = U0Ccos(ωt) V. Khi đó
 Xem đáp án
Xem đáp án
\({\varphi _i} = \frac{\pi }{2} > {\varphi _u}\). Chọn D
Câu 7:
Công thức xác định cường độ điện trường gây ra bởi điện tích Q, tại một điểm trong chân không, cách điện tích Q một khoảng r là?
 Xem đáp án
Xem đáp án
Chọn C
Câu 8:
 Xem đáp án
Xem đáp án
Chọn B
Câu 9:
Trong các thí nghiệm về giao thoa ánh sáng, khoảng vân i được tính bằng công thức nào?
 Xem đáp án
Xem đáp án
Chọn B
Câu 10:
Khi nói về sóng điện từ, phát biểu nào sau đây là sai?
 Xem đáp án
Xem đáp án
Sóng điện từ truyền được trong chân không. Chọn C
Câu 12:
Máy phát điện xoay chiều một pha có p cặp cực, số vòng quay của rôto là n (vòng/phút) thì tần số dòng điện xác định là:
 Xem đáp án
Xem đáp án
Chọn A
Câu 13:
Các Rocker kỳ cựu đã bị tổn hại thính giác cấp tính vì mức cường độ âm thanh cực cao mà họ phải chịu đựng trong nhiều năm. Nhiều Rocker bây giờ đã phải mang nút bịt lỗ tai để bảo vệ thính giác của bản thân khi biểu diễn (như hình bên). Nút bịt lỗ tai này có tác dụng gì?

 Xem đáp án
Xem đáp án
Chọn D
Câu 15:
Một con lắc đơn chiều dài ℓ dao động điều hòa tại nơi có gia tốc trọng trường với biên độ góc nhỏ. Chu kỳ dao động của nó là
 Xem đáp án
Xem đáp án
Chọn D
Câu 16:
Khoảng cách giữa hai điểm gần nhất trên phương truyền sóng dao động ngược pha bằng?
 Xem đáp án
Xem đáp án
Chọn C
Câu 18:
Trong y tế, để khử trùng không khí, tiệt trùng dụng cụ y tế và diệt khuẩn phòng mổ người ta thường sử dụng loại tia nào sau đây?
 Xem đáp án
Xem đáp án
Chọn D
Câu 19:
Điều kiện có sóng dừng trên dây chiều dài ℓ khi cả hai đầu dây cố định hay hai đầu tự do là?
 Xem đáp án
Xem đáp án
Chọn D
Câu 20:
Đặt điện áp xoay chiều u = U0cos(ωt) vào hai đầu đoạn mạch chứa điện trở thuần R mắc nối tiếp cuộn dây thuần cảm có hệ số tự cảm L. Biết R = 30Ω, ZL = 40Ω. Hệ số công suất của đoạn mạch bằng?
 Xem đáp án
Xem đáp án
\(\cos \varphi = \frac{R}{{\sqrt {{R^2} + Z_L^2} }} = \frac{{30}}{{\sqrt {{{30}^2} + {{40}^2}} }} = 0,6\). Chọn A
Câu 21:
Tại một nơi, chu kỳ dao động điều hòa của một con lắc đơn là T = 2 (s). Sau khi tăng chiều dài của con lắc thêm 21 cm thì chu kỳ dao động điều hòa của nó là 2,2 (s). Chiều dài ban đầu của con lắc là?
 Xem đáp án
Xem đáp án
\(T = 2\pi \sqrt {\frac{l}{g}} \Rightarrow \frac{{T'}}{T} = \sqrt {\frac{{l'}}{l}} \Rightarrow \frac{{2,2}}{2} = \sqrt {\frac{{l + 21}}{l}} \Rightarrow l = 100cm\). Chọn D
Câu 22:
Cho hạt nhân \({}_{13}^{27}Al\)(Nhôm) có mAl = 26,9972u. Biết khối lượng các nuclôn là mp = 1,0073u, mn = 1,0087u, 1u = 931,5 MeV/c2. Năng lượng liên kết của hạt nhân \({}_{13}^{27}Al\) nhận giá trị nào sau đây?
 Xem đáp án
Xem đáp án
\(\Delta m = 13{m_p} + 14{m_n} - {m_{Al}} = 13.1,0073 + 14.1,0087 - 26,9972 = 0,2195u\)
\({W_{lk}} = \Delta m{c^2} = 0,2195.931,5 \approx 204,5MeV\). Chọn A
Câu 23:
Mạch chọn sóng của một máy thu gồm một tụ điện có điện dung C = \(\frac{4}{{9{\pi ^2}}}\)pF và cuộn cảm có độ tự cảm biến thiên. Để có thể bắt được sóng điện từ có bước sóng 100 m thì độ tự cảm cuộn dây bằng bao nhiêu?
 Xem đáp án
Xem đáp án
\(\lambda = cT = c.2\pi \sqrt {LC} \Rightarrow 100 = {3.10^8}.2\pi \sqrt {L.\frac{4}{{9{\pi ^2}}}{{.10}^{ - 12}}} \Rightarrow L = 0,0625H\). Chọn C
Câu 24:
Trong thí nghiệm giao thoa ánh sáng dùng hai khe I-âng, biết D = 1 m, a = 1 mm. Khoảng cách từ vân sáng thứ 4 đến vân sáng thứ 10 ở cùng bên với vân trung tâm là 3,6 mm. Tính bước sóng ánh sáng?
 Xem đáp án
Xem đáp án
\(10i - 4i = 3,6 \Rightarrow i = 0,6mm\)
\(i = \frac{{\lambda D}}{a} \Rightarrow 0,6 = \frac{{\lambda .1}}{1} \Rightarrow \lambda = 0,6\mu m\). Chọn A
Câu 25:
Con lắc đơn gồm vật nặng treo vào một sợi dây dài ℓ = 0,8 m dao động điều hòa với biên độ góc 0,1 rad. Chọn gốc thế năng tại vị trí cân bằng. Lấy g = 10 m/s2. Tốc độ của vật nặng tại vị trí động năng bằng thế năng là?
 Xem đáp án
Xem đáp án
\({W_d} = {W_t} \Rightarrow v = \frac{{{v_{\max }}}}{{\sqrt 2 }} = \sqrt {gl\left( {1 - \cos {\alpha _0}} \right)} = \sqrt {10.0,8.\left( {1 - \cos 0,1} \right)} \approx 0,2m/s = 20cm/s\). Chọn D
Câu 26:
Hãy quan sát hình và cho biết gần đúng giá trị vận tốc truyền sóng trên dây. Biết tần số sóng là 100Hz, dây dài 1,5m?

 Xem đáp án
Xem đáp án
\(l = k.\frac{\lambda }{2} \Rightarrow 1,5 = 3.\frac{\lambda }{2} \Rightarrow \lambda = 1m\)
\(v = \lambda f = 100m/s\). Chọn B
Câu 27:
Mạch điện xoay chiều gồm RLC mắc nối tiếp, có R = 30 Ω, ZC = 20 Ω, ZL = 60 Ω. Tổng trở của mạch là?
 Xem đáp án
Xem đáp án
\(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} = \sqrt {{{30}^2} + {{\left( {60 - 20} \right)}^2}} = 50\Omega \). Chọn A
Câu 28:
Công thoát electrôn của một kim loại là 2,36 eV. Cho h = 6,625.10–34 J.s; c = 3.108 m/s; 1 eV = 1,6.10–19 J. Giới hạn quang điện của kim loại trên là?
 Xem đáp án
Xem đáp án
\(\lambda = \frac{{hc}}{A} = \frac{{1,{{9875.10}^{ - 25}}}}{{2,36.1,{{6.10}^{ - 19}}}} \approx 0,{53.10^{ - 6}} = 0,53\mu m\). Chọn B
Câu 29:
Một đoạn dây dẫn dài 0,80 m đặt nghiêng một góc 600 so với hướng của các đường sức từ trong một từ trường đều có cảm ứng từ 0,50 T. Khi dòng điện chạy qua đoạn dây dẫn này có cường độ 7,5 A, thì đoạn dây dẫn bị tác dụng một lực từ bằng bao nhiêu?
 Xem đáp án
Xem đáp án
\(F = IlB\sin \alpha = 7,5.0,8.0,5.\sin {60^o} \approx 2,6\) (N). Chọn C
Câu 30:
Một sợi dây đàn hồi căng ngang với hai đầu cố định. Sóng truyền trên dây có tốc độ không đổi nhưng tần số \[f\] thay đổi được. Khi \[f\] nhận giá trị 1760 Hz thì trên dây có sóng dừng với 4 bụng sóng. Giá của \[f\] để trên dây có sóng dừng với 3 bó sóng là?
 Xem đáp án
Xem đáp án
\(l = k.\frac{\lambda }{2} = \frac{{kv}}{{2f}} \Rightarrow \frac{k}{f} = const \Rightarrow \frac{4}{{1760}} = \frac{3}{f} \Rightarrow f = 1320Hz\). Chọn A
Câu 31:
Trong thí nghiệm giao thoa sóng ở mặt chất lỏng, hai nguồn kết hợp đặt tại A và B cách nhau 15 cm, dao động cùng pha theo phương thẳng đứng. Ở mặt chất lỏng, M là điểm cực đại giao thoa cách A và B lần lượt là 20 cm và 24,8 cm giữa M và đường trung trực của đoạn thẳng AB có bốn vân giao thoa cực tiểu khác. Gọi C và D là hai điểm trên mặt nước sao cho ABCD là hình vuông. Số điểm cực đại giao thoa trên đoạn thẳng CD là?
 Xem đáp án
Xem đáp án
\(\lambda = \frac{{MB - MA}}{k} = \frac{{24,8 - 20}}{4} = 1,2cm\)
\({k_C} = \frac{{CA - CB}}{\lambda } = \frac{{15\sqrt 2 - 15}}{{1,2}} \approx 5,2 \to \)trên CD có \(5.2 + 1 = 11\) cực đại. Chọn A
Câu 32:
Đặt điện áp xoay chiều có điện áp hiệu dụng U = 120V vào hai đầu đoạn mạch RLC nối tiếp thì cường độ dòng điện hiệu dụng qua mạch đo được là 1,2 A. Biết điện áp hai đầu đoạn mạch nhanh pha \[\frac{{2\pi }}{3}rad\]so với điện áp hai đầu mạch RC, điện áp hiệu dụng Giá trị điện trở thuần là?
 Xem đáp án
Xem đáp án
\({u_L} = u - {u_{RC}} = 120\angle \frac{{2\pi }}{3} - 120\angle 0 = 120\sqrt 3 \angle \frac{{5\pi }}{6} \Rightarrow {\varphi _i} = \frac{{5\pi }}{6} - \frac{\pi }{2} = \frac{\pi }{3}\)
\({U_R} = {U_{RC}}\cos {\varphi _{RC}} = 120\cos \frac{\pi }{3} = 60\) (V)
\(R = \frac{{{U_R}}}{I} = \frac{{60}}{{1,2}} = 50\Omega \). Chọn D
Câu 33:
Khi êlectron ở quỹ đạo dừng thứ n thì năng lượng của nguyên tử hiđrô được tính theo công thức En=-13,6/n2 (eV) (n = 1, 2, 3.). Khi êlectron trong nguyên tử hiđrô chuyển từ quỹ đạo dừng n = 3 sang quỹ đạo dừng n’ = 2 thì nguyên tử hiđrô phát ra phôtôn ứng với bức xạ có bước sóng bằng bao nhiêu?
 Xem đáp án
Xem đáp án
\(\varepsilon = {E_3} - {E_2} \Rightarrow \frac{{1,{{9875.10}^{ - 25}}}}{\lambda } = \left( { - \frac{{13,6}}{{{3^2}}} + \frac{{13,6}}{{{2^2}}}} \right).1,{6.10^{ - 19}} \Rightarrow \lambda \approx 0,{6576.10^{ - 6}}m = 0,6576\mu m\)
Chọn D
Câu 34:
Trong thí nghiệm của Young về giao thoa ánh sáng, khoảng cách giữa hai khe là 1,5 mm, khoảng cách giữa hai khe đến màn M là 2 m. Nguồn S chiếu đồng thời hai bức xạ đơn sắc có bước sóng λ1 = 0,48 µm và λ2 = 0,64 µm. Người ta thấy trên màn có những vân sáng có màu giống như màu của vân chính giữa cách đều nhau, khoảng cách ngắn nhất giữa 2 vân sáng có màu của vân sáng chính giữa cách nhau một đoạn là?
 Xem đáp án
Xem đáp án
\(i = \frac{{\lambda D}}{a} \Rightarrow {i_1} = \frac{{0,48.2}}{{1,5}} = 0,64mm\) và \({i_2} = \frac{{0,64.2}}{{1,5}} = \frac{{64}}{{75}}mm\)
\(\frac{{{i_1}}}{{{i_2}}} = \frac{{0,64}}{{64/75}} = \frac{3}{4} \Rightarrow {i_{12}} = 2,56mm\). Chọn B
Câu 35:
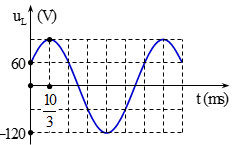
Đặt một điện áp xoay chiều vào hai đầu một đoạn mạch gồm điện trở \(R = 60\sqrt 3 \;\Omega \) mắc nối tiếp với một cuộn dây thuần cảm có độ tự cảm \(L = \frac{3}{{5\pi }}H\). Đồ thị biểu diễn sự phụ thuộc của điện áp \({u_L}\)theo thời gian như hình bên. Biểu thức điện áp giữa hai đầu đoạn mạch này là:
 Xem đáp án
Xem đáp án
\({u_L} = \frac{{{U_{0L}}}}{2} \uparrow \Rightarrow {\varphi _{{u_L}}} = - \frac{\pi }{3}\)
\(\omega = \frac{\alpha }{t} = \frac{{\pi /3}}{{\frac{{10}}{3}{{.10}^{ - 3}}}} = 100\pi \) (rad/s)
\({Z_L} = \omega L = 100\pi .\frac{3}{{5\pi }} = 60\Omega \)
\(u = \frac{{{u_L}}}{{{Z_L}j}}.\left( {R + {Z_L}j} \right) = \frac{{120\angle - \frac{\pi }{3}}}{{60j}}.\left( {60\sqrt 3 + 60j} \right) = 240\angle - \frac{{2\pi }}{3}\)\(O\). Chọn D
Câu 36:
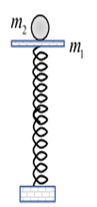
Một con lắc lò xo đặt thẳng đứng gồm lò xo nhẹ có độ cứng \(k = 100\,N/m\) và vật nhỏ \({m_1}\) khối lượng \(200\,g\). Một đầu lò xo gắn chặt vào sàn. Ban đầu, giữ \({m_1}\) ở vị trí lò xo nén \(12\,cm\) (trong giới hạn đàn hồi của lò xo) rồi đặt thêm vật nhỏ \({m_2}\) có khối lượng cũng bằng \(200\,g\) lên trên \({m_1}\) như hình bên. Thả nhẹ để các vật bắt đầu chuyển động theo phương thẳng đứng. Vào thời điểm \({t_1}\), vật \({m_2}\) rời khỏi \({m_1}\) chuyển động thẳng đứng lên trên, sau khi rời m1, m2 chuyển động ném lên đạt độ cao cực đại vào thời điểm \({t_2}\). Khoảng cách giữa 2 vật tại thời điểm \({t_2}\) có giá trị gần nhất với giá trị nào sau đây?
 Xem đáp án
Xem đáp án
GĐ1: Hai vật cùng dao động từ M lên đến vị trí tự nhiên
Tại vtcb O nén \(\Delta {l_0} = \frac{{\left( {{m_1} + {m_2}} \right)g}}{k} = \frac{{\left( {0,2 + 0,2} \right).10}}{{100}} = 0,04m = 4cm\)
\(A = 12 - 4 = 8cm\)
\(\omega = \sqrt {\frac{k}{{{m_1} + {m_2}}}} = \sqrt {\frac{{100}}{{0,2 + 0,2}}} = 5\sqrt {10} \) (rad/s)
\(v = \omega \sqrt {{A^2} - \Delta l_0^2} = 5\sqrt {10} .\sqrt {{8^2} - {4^2}} = 20\sqrt {30} \) (cm/s)
GĐ2: Tại vttn thì lực đàn hồi hướng xuống nên vật m2 tách khỏi m1
*Vật m2 bị ném lên thẳng đứng đến khi dừng lại lần đầu thì \(t = \frac{v}{g} = 0,02\sqrt {30} s\)
*Vật m1 dao động điều hòa quanh vị trí cân bằng mới O1 nén
\(\Delta {l_1} = \frac{{{m_1}g}}{k} = \frac{{0,2.10}}{{100}} = 0,02m = 2cm\) và \({\omega _1} = \sqrt {\frac{k}{{{m_1}}}} = \sqrt {\frac{{100}}{{0,2}}} = 10\sqrt 5 \) (rad/s)
\({A_1} = \sqrt {\Delta l_1^2 + {{\left( {\frac{v}{{{\omega _1}}}} \right)}^2}} = \sqrt {{2^2} + {{\left( {\frac{{20\sqrt {30} }}{{10\sqrt 5 }}} \right)}^2}} = 2\sqrt 7 cm\)
Chọn gốc tọa độ tại vị trí cân bằng mới O1, chiều dương hướng lên
\[\left\{ \begin{array}{l}{x_1} = {A_1}\cos \left( {{\omega _1}t - \arccos \frac{{\Delta {l_1}}}{{{A_1}}}} \right) = 2\sqrt 7 \cos \left( {10\sqrt 5 .0,02\sqrt {30} - \arccos \frac{2}{{2\sqrt 7 }}} \right) \approx 1,5865cm\\{x_2} = \Delta {l_1} + vt - \frac{1}{2}g{t^2} = 2 + 20\sqrt {30} .0,02\sqrt {30} - \frac{1}{2}.1000.{\left( {0,02\sqrt {30} } \right)^2} = 8cm\end{array} \right.\]
\({x_2} - {x_1} = 8 - 1,5865 = 6,4135cm\). Chọn B
Câu 37:
Trong thí nghiệm giao thoa sóng ở mặt chất lỏng, hai nguồn sóng kết hợp đặt tại S1 và S2 cách nhau 15 cm, dao động theo phương thẳng đứng với cùng phương trình u = 4cos10πt( mm). Biết tốc độ truyền sóng trên mặt chất lỏng là 15 cm/s. Coi biên độ sóng không đổi. Gọi M là điểm trên mặt chất lỏng sao cho M1S = 25 cm và MS2 = 20 cm. Trong khoảng S2M, hai điểm A và B lần lượt gần S2 nhất và xa S2 nhất đều có tốc độ dao động cực đại bằng 80π mm/s. Khoảng cách AB gần nhất với giá trị nào sau đây?
 Xem đáp án
Xem đáp án
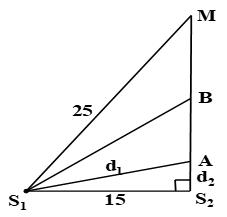
\(M{S_1}^2 = M{S_2}^2 + {S_1}{S_2}^2 \Rightarrow \Delta M{S_1}{S_2}\) vuông tại \({S_2}\)
\(\lambda = v.\frac{{2\pi }}{\omega } = 15.\frac{{2\pi }}{{10\pi }} = 3cm\) và \(A = \frac{{{v_{\max }}}}{\omega } = \frac{{80\pi }}{{10\pi }} = 8mm = 2a \to \)cực đại
Trên \(M{S_2}\) thì \(\frac{{M{S_1} - M{S_2}}}{\lambda } < k < \frac{{{S_1}{S_2}}}{\lambda } \Rightarrow \frac{{25 - 20}}{3} < k < \frac{{15}}{3}\)
\( \Rightarrow 1,7 < k < 5 \Rightarrow {k_A} = 4\) và \({k_B} = 2\)
\({d_1}^2 - {d_2}^2 = {S_1}{S_2}^2 \Rightarrow \left\{ \begin{array}{l}{d_1} - {d_2} = k\lambda \\{d_1} + {d_2} = \frac{{{S_1}{S_2}^2}}{{k\lambda }}\end{array} \right. \Rightarrow {d_2} = \frac{{{S_1}{S_2}^2}}{{2k\lambda }} - \frac{{k\lambda }}{2} = \frac{{{{15}^2}}}{{2k.3}} - \frac{{k.3}}{2} \Rightarrow \left\{ \begin{array}{l}k = 2 \Rightarrow {d_2} = 15,75cm\\k = 4 \Rightarrow {d_2} = 3,375cm\end{array} \right.\)
Vậy \(AB = 15,75 - 3,375 \approx 12,4cm\). Chọn B
Câu 38:
Cho một mẫu chất có chứa \(1,{31.10^{ - 8}}g\)chất phóng xạ 131X. Để xác định chu kì bán rã của chất phóng xạ này người ta dùng một máy đếm xung sử dụng đầu dò có đường kính 5,08 cm. Đặt đầu dò cách mẫu 50 cm để hứng tia phóng xạ. Sau 1 phút máy đếm được 1,68.106 xung. Biết mẫu chất phát ra tia phóng xạ tỏa đều theo mọi hướng và cứ 5 hạt trong chùm tia phóng xạ đập vào đầu dò thì máy đếm được 4 xung. Chu kì bán rã của 131X là
 Xem đáp án
Xem đáp án
Số hạt trên đường tròn bán kính \(R = 2,54cm\) là \(\frac{{1,{{68.10}^6}}}{4}.5 = 2,{1.10^6}\)
Số hạt trên mặt cầu bán kính \(r = 50cm\) là \(N = 2,{1.10^6}.\frac{{4\pi {r^2}}}{{\pi {R^2}}} = 2,{1.10^6}.4.{\left( {\frac{{50}}{{2,54}}} \right)^2} = {3255.10^6}\)
Số hạt ban đầu là \({N_0} = \frac{{{m_0}}}{A}.{N_A} = \frac{{1,{{31.10}^{ - 8}}}}{{131}}.6,{02.10^{23}} = 6,{02.10^{13}}\)
\(N = {N_0}\left( {1 - {2^{ - \frac{t}{T}}}} \right) \Rightarrow {3255.10^6} = 6,{02.10^{13}}\left( {1 - {2^{ - \frac{1}{T}}}} \right) \Rightarrow T = 12819ph \approx 8,9\)ngày. Chọn B
Câu 39:
Chọn phát biểu đúng khi nói so sánh pha của các đại lượng trong dòng điện xoay chiều?
 Xem đáp án
Xem đáp án
Chọn C
Câu 40:
Cho đoạn mạch gồm RLC mắc nối tiếp có R thay đổi, Giữa AM chỉ có R, MN có tụ C, NB có cuộn dây không thuần cảm. Đặt vào 𝐴, 𝐵 điện áp xoay chiều \(u = 30\sqrt {14} \cos \left( {\omega t} \right)(V)\) (với 𝜔 không thay đổi). Điện áp tức thời ở hai đầu đoạn mạch MB lệch pha 𝜋/3 so với dòng điện trong mạch. Khi giá trị biến trở 𝑅 = 𝑅1 thì công suất tiêu thụ trên biến trở là 𝑃 và điện áp hiệu dụng hai đầu đoạn mạch 𝑀𝐵 là 𝑈1. Khi giá trị biến trở là 𝑅 = 𝑅2 và 𝑅2 < 𝑅1 thì công suất tiêu thụ trên biến trở vẫn là 𝑃 và điện áp hiệu dụng hai đầu đoạn mạch 𝑀𝐵 là 𝑈2. Biết rằng 𝑈1 + 𝑈2 = 90 𝑉. Tỉ số 𝑅2/𝑅1 gần nhất với giá trị nào sau đây?
 Xem đáp án
Xem đáp án
\(\tan {\varphi _{rLC}} = \tan \frac{\pi }{3} = \sqrt 3 = \frac{{{Z_{LC}}}}{r}\). Chuẩn hóa \(\left\{ \begin{array}{l}{Z_{LC}} = \sqrt 3 \\r = 1\end{array} \right.\)
Hai giá trị R cho cùng \({P_R} \Rightarrow \) \({R_1}{R_2} = R_0^2 = {r^2} + Z_{LC}^2 = {1^2} + {\left( {\sqrt 3 } \right)^2} = 4\) (1)
\({U_1} + {U_2} = \frac{{U\sqrt {{r^2} + Z_{LC}^2} }}{{\sqrt {{{\left( {{R_1} + r} \right)}^2} + Z_{LC}^2} }} + \frac{{U\sqrt {{r^2} + Z_{LC}^2} }}{{\sqrt {{{\left( {{R_2} + r} \right)}^2} + Z_{LC}^2} }} \Rightarrow 90 = \frac{{30\sqrt 7 .2}}{{\sqrt {{{\left( {{R_1} + 1} \right)}^2} + 3} }} + \frac{{30\sqrt 7 .2}}{{\sqrt {{{\left( {{R_2} + 1} \right)}^2} + 3} }}\) (2)
Từ (1) và (2) \( \Rightarrow \left\{ \begin{array}{l}{R_2} = 1\\{R_1} = 4\end{array} \right. \Rightarrow \frac{{{R_2}}}{{{R_1}}} = 0,25\). Chọn B

