Cho , trên Ox lấy P, trên Oy lấy Q sao cho chu vi POQ bằng 2a không đổi. Chọn câu đúng
A. PQ luôn tiếp xúc với một đường tròn cố định
B. PQ không tiếp xúc với một đường tròn cố định nào
C. PQ = a
D. PQ = OP
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
Gọi I là giao điểm các tia phân giác của và A, B, C lần lượt là hình chiếu của I lên Ox, PQ và Oy
Vì I thuộc phân giác của góc xPQ nên IA = IB
Xét PAI và PBI có:
+ IA = IB (cmt)
+ Chung PI
+
nên PAI = PBI (cạnh huyền – cạnh góc vuông)
Suy ra PA = PB
Lí luận tương tự, ta có QB = QC.
OA + OC = OP + PA + OQ + QC = OP + PB + OQ + QB = OP + PQ + QO = 2a (do chu vi OPQ bằng 2a)
Vì IA = IB và IB = IC (cmt) nên IA = IC
Xét OAI và OCI có:
+ IA = IC (cmt)
+
+ cạnh chung OI
nên OAI = OCI (cạnh huyền – cạnh góc vuông)
Vì a không đổi và A, C thuộc tia Ox, Oy cố định nên A và C cố định
Do A và C lần lượt là hình chiếu của I lên Ox, Oy nên hai đường thẳng AI và CI cố định hay I cố định
Do I và A cố định nên độ dài đoạn thẳng AI không đổi
Do IA = IB (cmt) nên IB là bán kính của đường tròn (I; IA) mà IB PQ tại B nên PQ tiếp xúc với đường tròn (I; IA) cố định
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Từ một điểm A ở bên ngoài đường tròn (O; R), vẽ hai tiếp tuyến AB, AC với (O). Đường thẳng vuông góc với OB tại O cắt tia AC tại N. Đường thẳng vuông góc với OC cắt tia AB tại M. Tứ giác AMON là hình gì?
Cho hình chữ nhật ABCD, H là hình chiếu của A trên BD. M, N lần lượt là trung điểm của BH, CD. Đường nào sau đây là tiếp tuyến của đường tròn tâm A, bán kính AM?
Cho tam giác ABC có hai đường cao BD, CE cắt nhau tại H. Gọi M là trung điểm BC. Đường tròn (F) ở trên nhận các đường thẳng nào dưới đây là tiếp tuyến?
Cho tam giác ABC vuông tại A, đường cao AH. Đường tròn đường kính BH cắt AB tại D, đường tròn đường kính CH cắt AC tại E. Chọn khẳng định sai trong các khẳng định sau:
Cho đường tròn (O; 2cm) bán kính OB. Vẽ dây BC sao cho . Trên tia OB lấy điểm M sao cho BM = 2cm . Tính độ dài MC
Cho đường tròn (O), dây MN khác đường kính. Qua O kẻ đường vuông góc với MN, cắt tiếp tuyến tại M của đường tròn ở điểm P. Cho bán kính của đường tròn bằng 10cm; MN = 12cm. Tính OP
Cho tam giác ABC cân tại A; đường cao AH và BK cắt nhau tại I. Khi đó đường thẳng nào sau đây là tiếp tuyến của đường tròn đường kính AI?
Từ một điểm A ở bên ngoài đường tròn (O; R), vẽ hai tiếp tuyến AB, AC với (O). Đường thẳng vuông góc với OB tại O cắt tia AC tại N. Đường thẳng vuông góc với OC cắt tia AB tại M. Điểm A phải cách O một khoảng là bao nhiêu để cho MN là tiếp tuyến của (O)?
Cho nửa đường tròn đường kính AB, C là một điểm thuộc nửa đường tròn. Vẽ dây BD là phân giác góc ABC. BD cắt AC tại E, AD cắt BC tại G. H là điểm đối xứng với E qua D. Chọn câu đúng:
Cho đường tròn (O; 2cm) bán kính OB. Vẽ dây BC sao cho . Trên tia OB lấy điểm M sao cho BM = 2cm
Cho tam giác ABC có hai đường cao BD, CE cắt nhau tại H. Xác định tâm F của đường tròn đi qua bốn điểm A, D, H, E
Cho nửa đường tròn (O; R), AB là đường kính. Dây BC có độ dài R. Trên tia đối của tia CB lấy điểm D sao cho CD = 3R. Chọn câu đúng
Cho đường tròn (O), dây AB khác đường kính. Qua O kẻ đường vuông góc với AB, cắt tiếp tuyến tại A của đường tròn ở điểm C. Cho bán kính của đường tròn bằng 15cm; AB = 24cm. Tính OC
Cho đường tròn (O), dây MN khác đường kính. Qua O kẻ đường vuông góc với MN, cắt tiếp tuyến tại M của đường tròn ở điểm P. Chọn khẳng định đúng?
Cho đường tròn (O), dây AB khác đường kính. Qua O kẻ đường vuông góc với AB, cắt tiếp tuyến tại A của đường tròn ở điểm C. Chọn khẳng định đúng:
1. Dấu hiệu nhận biết tiếp tuyến của đường tròn
Hai dấu hiệu nhận biết tiếp tuyến đường tròn:
• Nếu một đường thẳng và một đường tròn chỉ có một điểm chung thì đường thẳng đó là tiếp tuyến của đường tròn.
• Nếu khoảng cách từ tâm của một đường tròn đến đường thẳng bằng bán kính của đường tròn thì đường thẳng đó là tiếp tuyến của đường tròn.
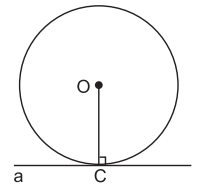
Ví dụ 1. Đường thẳng a và đường tròn (O) chỉ có một điểm chung là C.
Khi đó, đường thẳng a là tiếp tuyến của đường tròn (O).
2. Định lí
Định lí. Nếu một đường thẳng đi qua một điểm của một đường tròn và vuông góc với bán kính đi qua tiếp điểm thì đường thẳng ấy là một tiếp tuyến của đường tròn.
Ví dụ 2. Cho điểm H thuộc đường tròn (O). Đường thẳng Δ đi qua điểm H và Δ ⊥ OH
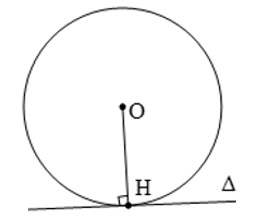
Khi đó, đường thẳng Δ là tiếp tuyến của đường tròn (O).