Tìm khẳng định đúng trong các khẳng định sau:
( I ) f(x) liên tục trên đoạn [ (a;b) ] và thì tồn tại ít nhất một số sao cho
(II) )Nếu f(x) liên tục trên đoạn và trên thì không liên tục trên
A. Chỉ (I)
B. Chỉ (II)
C. Cả (I) và (II) đúng
D. Cả (I) và (II) sai
 Giải bởi Vietjack
Giải bởi Vietjack

Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Hàm số có đồ thị dưới đây gián đoạn tại điểm có hoành độ bằng bao nhiêu?
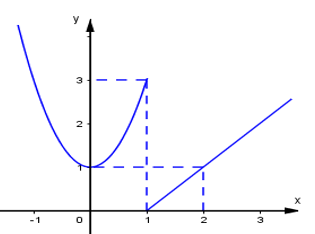
Cho hàm số f(x) xác định trên [a;b]. Trong các khẳng định sau, khẳng định nào đúng?
Cho hàm số . Phương trình có nghiệm thuộc khoảng nào trong các khoảng:
(I).
(II).
(III).
(IV).
Cho hàm số (f( x ) ) liên tục trên đoạn sao cho . Có thể nói gì về số nghiệm của phương trình trên đoạn :
I. HÀM SỐ LIÊN TỤC TẠI MỘT ĐIỂM
Định nghĩa 1
Cho hàm số y = f(x) xác định trên khoảng K và ∈ K.
Hàm số y = f(x) được gọi là liên tục tại x0 nếu
Ví dụ 1. Xét tính liên tục của hàm số tại = 2.
Giải
Hàm số đã cho xác định trên .
Do đó hàm số xác định trên khoảng chứa = 2. Khi đó ta có:
.
Vậy hàm số y = f(x) liên tục tại = 2.
II. HÀM SỐ LIÊN TỤC TRÊN MỘT KHOẢNG
Định nghĩa 2
Hàm số y = f(x) được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm của khoảng đó.
Hàm số y = f(x) được gọi là liên tục trên đoạn [a; b] nếu nó liên tục trên khoảng (a; b) và
Nhận xét: Đồ thị của hàm số liên tục trên một khoảng là một đường liền trên khoảng đó.
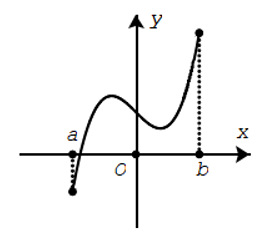
Hàm số liên tục trên khoảng (a;b)
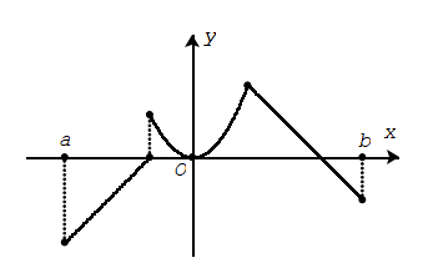
Hàm số không liên tục trên khoảng (a; b).
III. MỘT SỐ ĐỊNH LÍ CƠ BẢN
Định lí 1
a) Hàm số đa thức liên tục trên toàn bộ tập số thực .
b) Hàm số phân thức hữu tỉ và hàm số lượng giác liên tục trên từng khoảng xác định của chúng.
Định lí 2
Giả sử y = f(x) và y = g(x) là hai hàm số liên tục tại điểm x0. Khi đó:
a) Các hàm số y = f(x) + g(x), y = f(x) – g(x) và y = f(x).g(x) liên tục tại x0;
b) Hàm số liên tục tại x0 nếu g(x0) ≠ 0.
Ví dụ 2. Cho hàm số trên tập xác định của nó.
Giải
Tập xác định
- Nếu x = 3, ta có f(3) = 4,
Do đó f(x) liên tục tại x = 3.
- Nếu thì là hàm phân thức hữu tỉ nên liên tục trên các khoảng .
Vậy hàm số y = f(x) liên tục trên .
Định lí 3
Nếu hàm số y = f(x) liên tục trên đoạn [a;b] và f(a).f(b) < 0, thì tồn tại ít nhất một điểm c ∈ (a; b) sao cho f(c) = 0.
Định lí 3 có thể phát biểu theo một dạng khác như sau:
Nếu hàm số y = f(x) liên tục trên đoạn [a; b] và f(a).f(b) < 0, thì phương trình f(x) = 0 có ít nhất một nghiệm nằm trong khoảng (a, b).
Ví dụ 3. Chứng minh rằng phương trình x5 – 3x – 7 = 0 luôn có nghiệm.
Giải
Xét hàm f(x) = x5 – 3x – 7
Ta có: f(0) = - 7, f(2) = 19. Do đó f(0).f(2) = (-7).19 < 0.
Vì hàm số f(x) là hàm đa thức nên liên tục trên . Do đó hàm số f(x) liên tục trên [0;2]. Từ đó suy ra phương trình f(x) = 0 có ít nhất một nghiệm .
Vậy phương trình đã cho luôn có nghiệm.