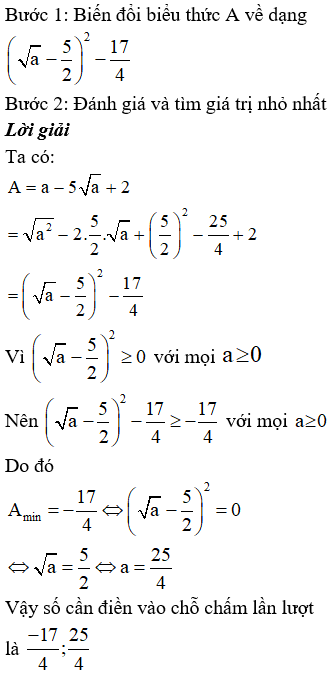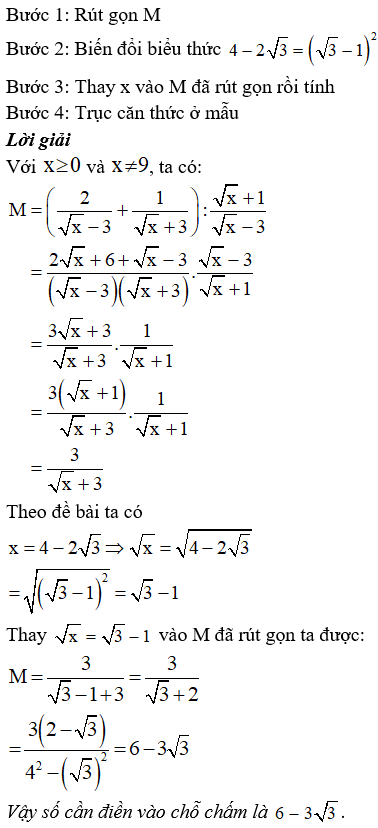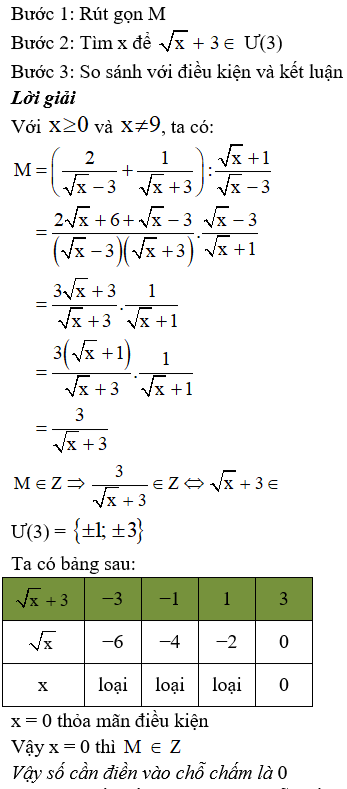20 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 9 Ôn tập chương I Đại số có đáp án (Thông hiểu)

Câu 1:

Rút gọn biểu thức

$(4 + \sqrt{15}) (\sqrt{10} - \sqrt{6}) \sqrt{4 - \sqrt{15}} = ...$

Xem đáp án

Bước 1: Áp dụng Quy tắc đưa thừa số vào trong dấu căn

Bước 2: Đưa biểu thức $\sqrt{10} - \sqrt{6}$ vào trong dấu căn và đưa biểu thức trong căn về dạng (A + B)²

Lời giải

Ta có:

$\begin{array}{l} (4 + \sqrt{15}) (\sqrt{10} - \sqrt{6}) \sqrt{4 - \sqrt{15}} \\ = \sqrt{{(4 + \sqrt{15})}^{2} (4 - \sqrt{15})} (\sqrt{10} - \sqrt{6}) \\ = \sqrt{(4^{2} + \sqrt{15^{2}}) (4 + \sqrt{15}) {(\sqrt{10} - \sqrt{6})}^{2}} \\ = \sqrt{(4 + \sqrt{15}) {[\sqrt{2} (\sqrt{5} - \sqrt{3})]}^{2}} \\ = \sqrt{2 (4 + \sqrt{15}) {(\sqrt{5} - \sqrt{3})}^{2}} \\ = \sqrt{(8 + 2 \sqrt{15}) {(\sqrt{5} - \sqrt{3})}^{2}} \\ = \sqrt{{(\sqrt{5} + \sqrt{3})}^{2} {(\sqrt{5} - \sqrt{3})}^{2}} \\ = \sqrt{{(5 - 3)}^{2}} \\ = 2 \end{array}$

Vậy số cần điền vào chỗ chấm là 2

Câu 2:

Lựa chọn đáp án đúng nhất

Với $x \geq 0; x \neq 9$ . Cho hai biểu thức $A = \frac{x + 3}{x - 9} + \frac{2}{\sqrt{x} + 3} - \frac{1}{\sqrt{x} - 3}$ và $B = \frac{\sqrt{x} + 1}{\sqrt{x} + 2}$

Rút gọn A được kết quả là:

A. $\frac{\sqrt{x} - 2}{\sqrt{x} - 3}$

B. $\frac{\sqrt{x} - 2}{\sqrt{x} + 3}$

C. $\frac{\sqrt{x} + 2}{\sqrt{x} - 3}$

D. $\frac{\sqrt{x} + 2}{\sqrt{x} + 3}$

Xem đáp án

Với $x \geq 0; x \neq 9$ . Ta có:

$\begin{array}{l} A = \frac{x + 3}{x - 9} + \frac{2}{\sqrt{x} + 3} - \frac{1}{\sqrt{x} - 3} \\ = \frac{x + 3 + 2 (\sqrt{x} - 3) - (\sqrt{x} + 3)}{(\sqrt{x} + 3) (\sqrt{x} - 3)} \\ = \frac{x + \sqrt{x} - 6}{(\sqrt{x} + 3) (\sqrt{x} - 3)} \\ = \frac{x - 2 \sqrt{x} + 3 \sqrt{x} - 6}{(\sqrt{x} + 3) (\sqrt{x} - 3)} \\ = \frac{(\sqrt{x} - 2) (\sqrt{x} + 3)}{(\sqrt{x} + 3) (\sqrt{x} - 3)} \\ = \frac{\sqrt{x} - 2}{\sqrt{x} - 3} \end{array}$

Đáp án cần chọn là: A

Câu 3:

Lựa chọn đáp án đúng nhất

Với $x \geq 0; x \neq 9$ . Cho hai biểu thức $A = \frac{x + 3}{x - 9} + \frac{2}{\sqrt{x} + 3} - \frac{1}{\sqrt{x} - 3}$ và $B = \frac{\sqrt{x} + 1}{\sqrt{x} + 2}$

Tìm x để A < 1

A. $x \geq 0$

B. x > 9

C. $0 \leq x < 9$

D. x < 9

Xem đáp án

Với $x \geq 0; x \neq 9$ . Ta có:

$\begin{array}{l} A = \frac{x + 3}{x - 9} + \frac{2}{\sqrt{x} + 3} - \frac{1}{\sqrt{x} - 3} \\ = \frac{x + 3 + 2 (\sqrt{x} - 3) - (\sqrt{x} + 3)}{(\sqrt{x} + 3) (\sqrt{x} - 3)} \\ = \frac{x + \sqrt{x} - 6}{(\sqrt{x} + 3) (\sqrt{x} - 3)} \\ = \frac{x - 2 \sqrt{x} + 3 \sqrt{x} - 6}{(\sqrt{x} + 3) (\sqrt{x} - 3)} \\ = \frac{(\sqrt{x} - 2) (\sqrt{x} + 3)}{(\sqrt{x} + 3) (\sqrt{x} - 3)} \\ = \frac{\sqrt{x} - 2}{\sqrt{x} - 3} \end{array}$

$\begin{array}{l} A < 1 \Leftrightarrow \frac{\sqrt{x} - 2}{\sqrt{x} - 3} < 1 \\ \Leftrightarrow \frac{\sqrt{x} - 2}{\sqrt{x} - 3} - 1 < 0 \\ \Leftrightarrow \frac{\sqrt{x} - 2 - \sqrt{x} + 3}{\sqrt{x} - 3} < 0 \\ \Leftrightarrow \frac{1}{\sqrt{x} - 3} < 0 \\ \Leftrightarrow \sqrt{x} - 3 < 0 (v i 1 > 0) \\ \Leftrightarrow \sqrt{x} < 3 \\ \Leftrightarrow x < 9 \end{array}$

Mà $x \geq 0; x \neq 9$ . Do đó A < 1 $\Leftrightarrow 0 \leq x < 9$

Đáp án cần chọn là: C

Câu 4:

Điền số thích hợp vào chỗ chấm

Với $x \geq 0; x \neq 9$ . Cho hai biểu thức $A = \frac{x + 3}{x - 9} + \frac{2}{\sqrt{x} + 3} - \frac{1}{\sqrt{x} - 3}$ và $B = \frac{\sqrt{x} + 1}{\sqrt{x} + 2}$

Với A = B thì x = …

Xem đáp án

Bước 1: Rút gọn A

Bước 2: Quy đồng và khử mẫu của phương trình A = B

Bước 3: Rút gọn phương trình và tìm nghiệm

Lời giải

Với $x \geq 0; x \neq 9$ . Ta có:

$\begin{array}{l} A = \frac{x + 3}{x - 9} + \frac{2}{\sqrt{x} + 3} - \frac{1}{\sqrt{x} - 3} \\ = \frac{x + 3 + 2 (\sqrt{x} - 3) - (\sqrt{x} + 3)}{(\sqrt{x} + 3) (\sqrt{x} - 3)} \\ = \frac{x + \sqrt{x} - 6}{(\sqrt{x} + 3) (\sqrt{x} - 3)} \\ = \frac{x - 2 \sqrt{x} + 3 \sqrt{x} - 6}{(\sqrt{x} + 3) (\sqrt{x} - 3)} \\ = \frac{(\sqrt{x} - 2) (\sqrt{x} + 3)}{(\sqrt{x} + 3) (\sqrt{x} - 3)} \\ = \frac{\sqrt{x} - 2}{\sqrt{x} - 3} \end{array}$

Do đó $A = B \Leftrightarrow \frac{\sqrt{x} - 2}{\sqrt{x} - 3} = \frac{\sqrt{x} + 1}{\sqrt{x} + 2}$

$\begin{array}{l} \Leftrightarrow \frac{(\sqrt{x} - 2) (\sqrt{x} + 2)}{(\sqrt{x} - 3) (\sqrt{x} + 2)} = \frac{(\sqrt{x} + 1) (\sqrt{x} - 3)}{(\sqrt{x} + 2) (\sqrt{x} - 3)} \\ \Rightarrow (\sqrt{x} - 2) (\sqrt{x} + 2) = (\sqrt{x} + 1) (\sqrt{x} - 3) \\ \Leftrightarrow x - 4 = x - 2 \sqrt{x} - 3 \\ \Leftrightarrow 2 \sqrt{x} = 1 \\ \Leftrightarrow \sqrt{x} = \frac{1}{2} \\ \Leftrightarrow x = \frac{1}{4} (T M) \end{array}$

Vậy số cần điền vào chỗ chấm là $\frac{1}{4}$

Câu 5:

Lựa chọn đáp án đúng nhất:

Kết quả rút gọn của biểu thức $\frac{1}{\sqrt[3]{9} + \sqrt[3]{15} + \sqrt[3]{25}} + \frac{\sqrt[3]{81}}{3}$ là:

A. $\sqrt[3]{5}$

B. $\sqrt[3]{5} + \sqrt[3]{3}$

C. $\frac{\sqrt[3]{5} - \sqrt[3]{3}}{2}$

D. $\frac{\sqrt[3]{5} + \sqrt[3]{3}}{2}$

Xem đáp án

Bước 1: Nhân cả tử và mẫu của phân thức thứ nhất với biểu thức liên hợp của mẫu

Bước 2: Quy đồng và rút gọn

Lời giải

Ta có:

$\begin{array}{l} \frac{1}{\sqrt[3]{9} + \sqrt[3]{15} + \sqrt[3]{25}} + \frac{\sqrt[3]{81}}{3} \\ = \frac{(\sqrt[3]{5} - \sqrt[3]{3})}{(\sqrt[3]{9} + \sqrt[3]{15} + \sqrt[3]{25}) (\sqrt[3]{5} - \sqrt[3]{3})} + \frac{3 \sqrt[3]{3}}{3} \\ = \frac{\sqrt[3]{5} - \sqrt[3]{3}}{\sqrt[3]{5^{3}} - \sqrt[3]{3^{3}}} + \sqrt[3]{3} \\ = \frac{\sqrt[3]{5} - \sqrt[3]{3}}{2} + \sqrt[3]{3} \\ = \frac{\sqrt[3]{5} + \sqrt[3]{3}}{2} \end{array}$

Đáp án cần chọn là: D

*Lưu ý: $\frac{1}{\sqrt[3]{a^{2}} + \sqrt[3]{a b} + \sqrt[3]{b^{2}}} = \frac{\sqrt[3]{a} - \sqrt[3]{b}}{(\sqrt[3]{a} - \sqrt[3]{b}) (\sqrt[3]{a^{2}} + \sqrt[3]{a b} + \sqrt[3]{b^{2}})} = \frac{\sqrt[3]{a} - \sqrt[3]{b}}{a - b}$

Câu 6:

Điền số thích hợp vào chỗ chấm

Rút gọn biểu thức $\sqrt{16 - 6 \sqrt{7}} + \sqrt{29 + 4 \sqrt{7}} = ...$

Xem đáp án

Ta có:

$\sqrt{16 - 6 \sqrt{7}} + \sqrt{29 + 4 \sqrt{7}}$

$\begin{array}{l} = \sqrt{3^{2} - 2.3. \sqrt{7} + \sqrt{7^{2}}} + \sqrt{{(2 \sqrt{7})}^{2} + 2.2 \sqrt{7} .1 + 1^{2}} \\ = \sqrt{{(3 - \sqrt{7})}^{2}} + \sqrt{{(2 \sqrt{7} + 1)}^{2}} \\ = 3 - \sqrt{7} + 2 \sqrt{7} + 1 (v i 3 > \sqrt{7}) \\ = 4 + \sqrt{7} \end{array}$

Vậy số cần điền vào chỗ chấm là $4 + \sqrt{7}$ .

*Lưu ý: Với A là một biểu thức, ta có $\sqrt{A^{2}} = |A| = \{\begin{cases} A k h i A \geq 0 \\ - A k h i A < 0 \end{cases}$

Câu 7:

Khẳng định sau Đúng hay Sai?

Với a > 0; b > 0 và $a \neq b$ . Rút gọn biểu thức $\frac{a + b - 2 \sqrt{a b}}{\sqrt{a} - \sqrt{b}} : \frac{1}{\sqrt{a} + \sqrt{b}} = a - b$

A. Đúng.

B. Sai.

Xem đáp án

Bước 1: Biến đổi vế trái

Bước 2: Áp dụng hằng đẳng thức (a – b)(a + b) = a² – b² và rút gọn

Lời giải

Ta có:

Vế trái = $\frac{a + b - 2 \sqrt{a b}}{\sqrt{a} - \sqrt{b}} : \frac{1}{\sqrt{a} + \sqrt{b}}$

$\begin{array}{l} = \frac{{(\sqrt{a} - \sqrt{b})}^{2}}{\sqrt{a} - \sqrt{b}} . (\sqrt{a} + \sqrt{b}) \\ = (\sqrt{a} - \sqrt{b}) (\sqrt{a} + \sqrt{b}) \end{array}$

= a – b = Vế phải

Do đó khẳng định trên là Đúng

Đáp án cần chọn là: A

Câu 8:

Điền số thích hợp vào chỗ chấm

Biết $\sqrt{13 - 4 \sqrt{3}} = a + b \sqrt{3}$ (với $a, b \in ℤ$ ). Khi đó a – b = …

Xem đáp án

Bước 1: Biến đổi biểu thức dưới dấu căn về ${(2 \sqrt{3} - 1)}^{2}$ .

Bước 2: Áp dụng hằng đẳng thức $\sqrt{A^{2}} = |A|$ và đồng nhất hệ số để tìm a, b

Lời giải

Ta có:

$\begin{array}{l} \sqrt{13 - 4 \sqrt{3}} \\ = \sqrt{{(2 \sqrt{3})}^{2} - 2.2 \sqrt{3} .1 + 1^{2}} \\ = \sqrt{{(2 \sqrt{3} - 1)}^{2}} \\ = 2 \sqrt{3} - 1 (v i 2 \sqrt{3} > 1) \end{array}$

Mà $\sqrt{13 - 4 \sqrt{3}} = a + b \sqrt{3} = 2 \sqrt{3} - 1$

Vì $a, b \in ℤ$ nên ta có: a = −1; b = 2

Do đó a – b = −1 – 2 = −3

Vậy số cần điền vào chỗ chấm là −3

Câu 9:

Điền số thích hợp vào chỗ chấm

Cho $a \geq 0$ . Tìm giá trị nhỏ nhất của biểu thức $A = a - 5 \sqrt{a} + 2$

Đáp số A_min = … khi a = … (kết quả viết dưới dạng phân số)

Xem đáp án

Câu 10:

Điền số thích hợp vào chỗ chấm

Thực hiện phép tính $\frac{(\sqrt{3} + 1) (4 - 2 \sqrt{3})}{\sqrt{3} - 1} = ...$

Xem đáp án

Đưa $4 - 2 \sqrt{3}$ về dạng (a – b)², sau đó rút gọn biểu thức

Lời giải

Ta có:

$\begin{array}{l} \frac{(\sqrt{3} + 1) (4 - 2 \sqrt{3})}{\sqrt{3} - 1} \\ = \frac{(\sqrt{3} + 1) {(\sqrt{3} - 1)}^{2}}{\sqrt{3} - 1} \\ = (\sqrt{3} + 1) (\sqrt{3} - 1) \\ = {(\sqrt{3})}^{2} - 1^{2} \\ = 3 - 1 = 2 \end{array}$

Vậy số cần điền vào chỗ chấm là 2

Câu 11:

Điền số thích hợp vào chỗ chấm

Giải phương trình $\frac{2}{3} \sqrt{9 x - 27} + \sqrt{x - 3} = 6 + \sqrt{4 x - 12}$

Tập nghiệm của phương trình là S = {…}

Xem đáp án

Câu 12:

Lựa chọn đáp án đúng nhất

Với $x \geq 0$ và $x \neq 9$ . Cho biểu thức $M = (\frac{2}{\sqrt{x} - 3} + \frac{1}{\sqrt{x} + 3}) : \frac{\sqrt{x} + 1}{\sqrt{x} - 3}$

Rút gọn M được kết quả là:

A. $- \frac{3}{\sqrt{x} + 3}$

B. $\frac{3}{\sqrt{x} + 3}$

C. $\frac{\sqrt{x} + 1}{\sqrt{x} + 3}$

D. $\frac{\sqrt{x} + 1}{\sqrt{x} - 3}$

Xem đáp án

Rút gọn biểu thức trong ngoặc trước:

Mẫu thức chung $(\sqrt{x} - 3) (\sqrt{x} + 3)$

Lời giải

Với $x \geq 0$ và $x \neq 9$ , ta có:

$\begin{array}{l} M = (\frac{2}{\sqrt{x} - 3} + \frac{1}{\sqrt{x} + 3}) : \frac{\sqrt{x} + 1}{\sqrt{x} - 3} \\ = \frac{2 \sqrt{x} + 6 + \sqrt{x} - 3}{(\sqrt{x} - 3) (\sqrt{x} + 3)} . \frac{\sqrt{x} - 3}{\sqrt{x} + 1} \\ = \frac{3 \sqrt{x} + 3}{\sqrt{x} + 3} . \frac{1}{\sqrt{x} + 1} \\ = \frac{3 (\sqrt{x} + 1)}{\sqrt{x} + 3} . \frac{1}{\sqrt{x} + 1} \\ = \frac{3}{\sqrt{x} + 3} \end{array}$

Đáp án cần chọn là: B

Câu 13:

Điền số thích hợp vào chỗ chấm

Với $x \geq 0$ và $x \neq 9$ . Cho biểu thức $M = (\frac{2}{\sqrt{x} - 3} + \frac{1}{\sqrt{x} + 3}) : \frac{\sqrt{x} + 1}{\sqrt{x} - 3}$

Với $x = 4 - 2 \sqrt{3}$ thì M = …

Xem đáp án

Câu 14:

Điền số thích hợp vào chỗ chấm

Với $x \geq 0$ và $x \neq 9$ . Cho biểu thức $M = (\frac{2}{\sqrt{x} - 3} + \frac{1}{\sqrt{x} + 3}) : \frac{\sqrt{x} + 1}{\sqrt{x} - 3}$

Tìm $x \in ℤ$ để $M \in ℤ$

Đáp số: x = …

Xem đáp án

Câu 15:

Điền số thích hợp vào chỗ chấm

Giải phương trình $\sqrt{8 x - 12} + \sqrt{18 x - 27} = 12 - \sqrt{2 x - 3}$

Tập nghiệm của phương trình là S = {…}

Xem đáp án

Câu 16:

Điền số thích hợp vào chỗ chấm

Tính $\frac{1}{\sqrt{2} - 1} - \frac{3 \sqrt{6} - 3 \sqrt{10}}{\sqrt{3} - \sqrt{5}} = ...$

Xem đáp án

Ta có:

$\begin{array}{l} \frac{1}{\sqrt{2} - 1} - \frac{3 \sqrt{6} - 3 \sqrt{10}}{\sqrt{3} - \sqrt{5}} \\ = \frac{\sqrt{2} + 1}{{(\sqrt{2})}^{2} - 1} - \frac{3 \sqrt{2} (\sqrt{3} - \sqrt{5})}{\sqrt{3} - \sqrt{5}} \\ = \sqrt{2} + 1 - 3 \sqrt{2} \\ = 1 - 2 \sqrt{2} \end{array}$

Vậy số cần điền vào chỗ chấm là $1 - 2 \sqrt{2}$ .

Câu 17:

Điền số thích hợp vào chỗ chấm

Cho hai biểu thức $A = \sqrt{11} - \sqrt{10}$ và $B = \sqrt{4} - \sqrt{3}$

So sánh A … B

Xem đáp án

Bước 1: Nhân cả tử và mẫu của A, B với biểu thức liên hợp

Bước 2: So sánh A và B

Áp dụng tính chất nếu a > b thì $\frac{1}{a} < \frac{1}{b}$

Lời giải

Ta có:

$A = \sqrt{11} - \sqrt{10} = \frac{(\sqrt{11} - \sqrt{10}) (\sqrt{11} + \sqrt{10})}{\sqrt{11} + \sqrt{10}} = \frac{1}{\sqrt{11} + \sqrt{10}}$

$B = \sqrt{4} - \sqrt{3} = \frac{(\sqrt{4} - \sqrt{3}) (\sqrt{4} + \sqrt{3})}{\sqrt{4} + \sqrt{3}} = \frac{1}{\sqrt{4} + \sqrt{3}}$

Mà $\sqrt{4} < \sqrt{11}; \sqrt{3} < \sqrt{10} \Rightarrow \sqrt{11} + \sqrt{10} > \sqrt{4} + \sqrt{3}$

Do đó $\frac{1}{\sqrt{11} + \sqrt{10}} < \frac{1}{\sqrt{4} + \sqrt{3}} \Leftrightarrow \sqrt{11} - \sqrt{10} < \sqrt{4} - \sqrt{3}$

Vậy dấu cần điền là <

Câu 18:

Lựa chọn đáp án đúng nhất

Biểu thức $2 \sqrt{x + 5} + x \sqrt{4 - x}$ có nghĩa khi:

A. $x \geq 4$

B. $x \leq - 5$

C. $- 5 \leq x \leq 4$

D. $x \geq 4$ hoặc $x \leq - 5$

Xem đáp án

Biểu thức có nghĩa khi

$\{\begin{cases} x + 5 \geq 0 \\ 4 - x \geq 0 \end{cases} \Leftrightarrow \{\begin{cases} x \geq - 5 \\ x \leq 4 \end{cases} \Leftrightarrow - 5 \leq x \leq 4$

Đáp án cần chọn là: C

Câu 19:

Lựa chọn đáp án đúng nhất

Kết quả phép tính $\sqrt{7 + \sqrt{24} . \sqrt{7 - 2 \sqrt{6}}}$ là:

A. $\sqrt{49 + 7 \sqrt{24} - 14 \sqrt{6}}$

B. 25

C. 5

D. $\sqrt{5}$

Xem đáp án

Áp dụng quy tắc nhân hai căn thức và sử dụng hằng đẳng thức

Lời giải

Ta có:

$\begin{array}{l} \sqrt{7 + \sqrt{24} . \sqrt{7 - 2 \sqrt{6}}} \\ = \sqrt{7 + 2 \sqrt{6}} . \sqrt{7 - 2 \sqrt{6}} \\ = \sqrt{(7 + 2 \sqrt{6}) (7 - 2 \sqrt{6})} \\ = \sqrt{7^{2} - {(2 \sqrt{6})}^{2}} \\ = \sqrt{25} \\ = 5 \end{array}$

Đáp án cần chọn là: C

Câu 20:

Lựa chọn đáp án đúng nhất

Điều kiện xác định của biểu thức $\sqrt{2 x - 1} + \frac{x - 1}{x - 6}$ là:

A. $x \geq \frac{1}{2}$ và $x \neq 6$

B. $x \geq - \frac{1}{2}$ và $x \neq 6$

C. $x \geq \frac{1}{2}$ và x > 6

D. $x \geq \frac{1}{2}$ và $x \neq 1$

Xem đáp án

Điều kiện xác định:

$\{\begin{cases} 2 x - 1 \geq 0 \\ x - 6 \neq 0 \end{cases} \Leftrightarrow \{\begin{cases} x \geq \frac{1}{2} \\ x \neq 6 \end{cases}$

Đáp án cần chọn là: A

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Ôn tập chương I Đại số có đáp án

Trắc nghiệm Toán 9 Ôn tập chương I Đại số có đáp án (Thông hiểu)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương