Một người vay ngân hàng một số tiền với lãi suất mỗi tháng là 1,12%. Biết cuối mỗi tháng người đó phải trả cho ngân hàng 3.00.000 đồng và trả trong 1 năm thì hết nợ. Số tiền người đó vay là:
A. 33510627 đồng
B. 50341123 đồng
C. 30453210 đồng
D. 29340240 đồng
 Giải bởi Vietjack
Giải bởi Vietjack
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Thầy C gửi 5 triệu đồng vào ngân hàng với lãi suất 0,7%/tháng. Chưa đầy một năm thì lãi suất tăng lên thành 1,15%/tháng. Tiếp theo, sáu tháng sau lãi suất chỉ còn 0,9%/tháng. Thầy C tiếp tục gửi thêm một số tháng nữa rồi rút cả vốn lẫn lãi được 5787710,707 đồng. Hỏi thầy C đã gửi tổng thời gian bao nhiêu tháng?
Ông An gửi 320 triệu đồng vào ngân hàng ACB và VietinBank theo phương thức lãi kép. Số tiền thứ nhất gửi vào ngân hàng ACB với lãi suất 2,1% một quý trong thời gian 15 tháng. Số tiền còn lại gửi vào ngân hàng Vietinbank với lãi suất 0,73% một tháng trong thời gian 9 tháng. Biết tổng số tiền lãi ông An nhận được ở hai ngân hàng là 26670725,95 đồng. Hỏi số tiền ông An lần lượt ở hai ngân hàng ACB và VietinBank là bao nhiêu (số tiền được làm tròn tới hàng đơn vị)?
Một người lần đầu gửi vào ngân hàng 100 triệu đồng với kì hạn 3 tháng, lãi suất 2% một quý theo hình thức lãi kép. Sau đúng 6 tháng, người đó gửi thêm 100 triệu đồng với kì hạn và lãi suất như trước đó. Tổng số tiền người đó nhận được sau 1 năm gửi thêm tiền gần nhất với kết quả nào sau đây?
Bà Hoa gửi 100 triệu vào tài khoản định kì tính lãi suất là 8% một năm. Sau 5 năm, bà rút toàn bộ số tiền và dùng một nửa để sửa nhà, còn một nửa tiền bà lại đem gửi ngân hàng trong 5 năm với cùng lãi suất. Tính số tiền lãi thu được sau 10 năm.
Một sinh viên ra trường đi làm ngày 1/1/2020 với mức lương khởi điểm là a đồng mỗi tháng và cứ sau 2 năm lại được tăng thêm 10% và chi tiêu hàng tháng của anh ta là 40% lương. Anh ta dự định mua một căn hộ chung cư giá rẻ có giá trị tại thời điểm 1/1/2020 là 1 tỷ đồng và cũng sau 2 năm thì giá trị căn hộ tăng thêm 5%. Với a bằng bao nhiêu thì sau đúng 10 năm anh ta mua được căn hộ đó, biết rằng mức lương và mức tăng giá trị ngôi nhà là không đổi (kết quả quy tròn đến hàng nghìn đồng)
Ông Tuấn gửi 9,8 triệu đồng với lãi suất 8,4 %/năm và lãi hàng năm được nhập vào vốn. Hỏi theo cách đó thì sau bao nhiêu năm người đó thu được tổng số 20 triệu đồng (biết lãi suất không thay đổi)
Một người vay ngân hàng 100 triệu đồng với lãi suất hàng năm là 12%/năm. Sau tháng đầu tiên, mỗi tháng người đó đều trả 10 triệu đồng. Hỏi sau 6 tháng người đó còn nợ ngân hàng bao nhiêu?
Một người mỗi tháng đều đặn gửi vào ngân hàng một khoản tiền T theo hình thức lãi kép với lãi suất 0,6% mỗi tháng. Biết sau 15 tháng người đó có số tiền là 10 triệu đồng. Hỏi số tiền T gần với số tiền nào nhất trong các số sau.
Ông tuấn gửi tiết kiệm với lãi suất 8,4%/năm và lãi hàng năm được nhập vào vốn. Hỏi sau bao nhiêu năm người đó thu được gấp đôi số tiền ban đầu?
Biết thể tích khí năm 1998 là . 10 năm tiếp theo, mỗi năm thể tích tăng m%, 10 năm tiếp nữa, thể tích mỗi năm tăng n%. Tính thể tích năm 2018?
Ông An lập cuốn sổ tiết kiệm ở một ngan hàng số tiền gốc ban đầu là 200 triệu đồng với lãi suất cố định 0,54%/tháng. Cứ đều đặn sau mỗi tháng, kể từ ngày gửi, ông An rút 5 triệu ra để chi phí cho sinh họat gia đình. Biết rằng mỗi tháng ngân hàng tính lãi cho ông An theo số tiền còn lại. Hỏi sau đúng 3 năm, số tiền còn lại trong ngân hàng của ông An gần nhất với số tiền nào dưới đây?
Một người gửi vào ngân hàng số tiền A đồng, lãi suất r% mỗi tháng theo hình thức lãi kép, gửi theo phương thức có kì hạn 1 năm. Công thức tính số tiền cả vốn lẫn lãi mà người đó có sau 2 năm là:
Một người gửi vào ngân hàng số tiền A đồng, lãi suất r% mỗi tháng theo hình thức lãi kép, gửi theo phương thức có kì hạn 3 tháng. Công thức tính số tiền cả vốn lẫn lãi mà người đó có sau 2 năm là:
I. Khái niệm
– Hàm số , với , được gọi là hàm số lũy thừa.
Ví dụ 1. Các hàm số là những hàm số lũy thừa.
– Chú ý:
Tập xác định của hàm số lũy thừa tùy thuộc vào giá trị của α. Cụ thể:
+ Với α nguyên dương, tập xác định là R.
+ Với α nguyên âm hoặc bằng 0; tập xác định là .
+ Với α không nguyên, tập xác định là .
II. Đạo hàm của hàm số lũy thừa
– Hàm số lũy thừa có đạo hàm với mọi x > 0 và .
– Ví dụ 2.
a)
b) .
– Chú ý: Công thức tính đạo hàm của hàm hợp đối với hàm số lũy thừa có dạng:
– Ví dụ 3. Tính đạo hàm của hàm số .
Lời giải:
Ta có:
III. Khảo sát hàm số lũy thừa y = xα
Tập xác định của hàm số lũy thừa luôn chứa khoảng với . Trong trường hợp tổng quát, ta khảo sát hàm số trên khoảng này (gọi là tập khảo sát).
|
1. Tập khảo sát: 2. Sự biến thiên . Giới hạn đặc biệt: Tiệm cận: Không có
3. Bảng biến thiên
4. Đồ thị (với α > 0) |
1. Tập khảo sát: 2. Sự biến thiên Giới hạn đặc biệt: Tiệm cận: Trục Ox là tiệm cận ngang. Trục Oy là tiệm cận đứng của đồ thị. 3. Bảng biến thiên.
4. Đồ thị (với α < 0)
|
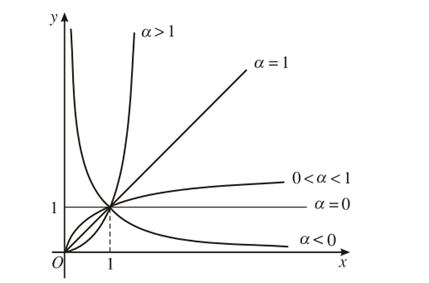
Đồ thị của hàm số lũy thừa y = xα luôn đi qua điểm (1; 1).
– Chú ý: Khi khảo sát hàm số lũy thừa với số mũ cụ thể, ta phải xét hàm số đó trên toàn bộ tập xác định của nó.
Ví dụ 4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số .
Lời giải:
1. Tập xác định:
2. Sự biến thiên.
Chiều biến thiên
Ta có: y’ < 0 trên khoảng nên hàm số đã cho nghịch biến.
Tiệm cận:
Đồ thị có tiệm cận ngang là trục hoành và có tiệm cận đứng là trục tung.
Bảng biến thiên
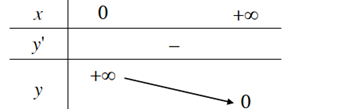
3. Đồ thị
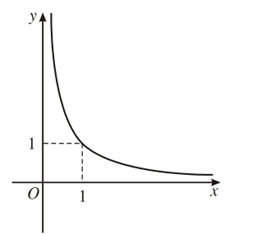
Bảng tóm tắt các tính chất của hàm số lũy thừa trên khoảng .
|
|
α > 0 |
|
|
Đạo hàm |
|
|
|
Chiều biến thiên |
Hàm số luôn đồng biến |
Hàm số luôn nghịch biến |
|
Tiệm cận |
Không có |
Tiệm cận ngang là trục Ox; Tiệm cận đứng là trục Oy |
|
Đồ thị |
Đồ thị luôn đi qua điểm (1; 1). |
|