Cho hình chóp tứ giác đều có cạnh đáy bằng a và góc hợp bởi một cạnh bên và mặt đáy bằng α . Khoảng cách từ tâm của đáy đến một cạnh bên bằng
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
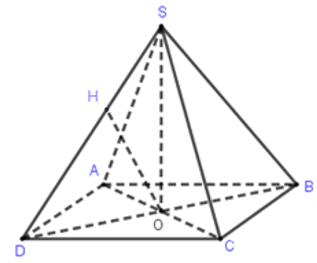
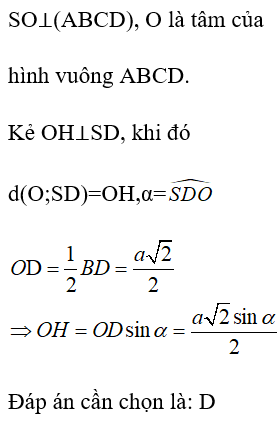
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tứ diện SABC trong đó SA, SB, SC vuông góc với nhau từng đôi một và SA = 3a, SB = a,SC = 2a. Khoảng cách từ A đến đường thẳng BC bằng:
Cho hình chóp A.BCD có cạnh AC vuông góc (BCD) và BCD là tam giác đều cạnh bằng a. Biết AC=, khoảng cách từ A đến đường thẳng BD bằng:
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách từ đỉnh A của hình lập phương đó đến đường thẳng DB' bằng
Cho hình chóp S.ABCD có SA vuông góc (ABCD), đáy ABCD là hình thoi cạnh bằng a và . Biết SA = 2a. Tính khoảng cách từ A đến SC.
Cho hình chóp S.ABCD có SA vuông góc (ABCD), SA = 2a, ABCD là hình vuông cạnh bằng a. Gọi O là tâm của ABCD, tính khoảng cách từ O đến SC.
Cho hình chóp S.ABC trong đó SA, AB, BC vuông góc với nhau từng đôi một. Biết SA = 3a, AB = , BC = . Khoảng cách từ B đến SC bằng
Cho hình chóp S.ABCD trong đó SA,AB,BC đôi một vuông góc và SA = AB = BC = 1. Khoảng cách giữa hai điểm S và C nhận giá trị nào trong các giá trị sau ?
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng đáy. Gọi M là trung điểm của CD. Khoảng cách từ M đến SA nhận giá trị nào trong các giá trị sau?
Cho hình chóp A.BCD có cạnh và BCD là tam giác đều cạnh bằng a. Biết và M là trung điểm của BD. Khoảng cách từ C đến đường thẳng AM bằng
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách từ đỉnh A của hình lập phương đó đến đường thẳng CD' bằng
Cho hình chóp S.ABC có đáy ABC là tam giác cạnh BC = a, AC = , góc . Cạnh bên SB vuông góc với mặt phẳng (ABC). Tính khoảng cách từ điểm A đến mặt phẳng (SBC).
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách từ ba điểm nào sau đây đến đường chéo AC' bằng nhau ?
Cho hình chóp A.BCD có cạnh AC vuông góc (BCD) và BCD là tam giác đều cạnh bằng a. Biết AC = và M là trung điểm của BD. Khoảng cách từ C đến đường thẳng AM bằng
Hình chóp đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Gọi H là trung điểm của BC, khoảng cách từ S đến AH bằng:
I. Khoảng cách từ một điểm đến một đường thẳng, một mặt phẳng.
1. Khoảng cách từ một điểm đến một đường thẳng
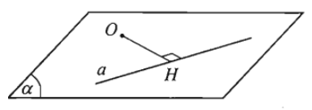
Cho điểm O và đường thẳng a. Trong mặt phẳng (O; a), gọi H là hình chiếu vuông góc của O lên a. Khi đó, khoảng cách giữa hai điểm O và H được gọi là khoảng cách từ điểm O đến đường thẳng a.
Kí hiệu: d(O; a).
Ví dụ 1. Cho hình lập phương ABCD. A'B'C'D' cạnh a. Tính khoảng cách từ B tới đường thẳng DB'.
Lời giải:
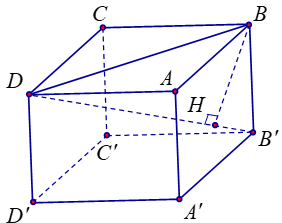
Từ giả thuyết ta suy ra:
Gọi H là hình chiếu của B lên DB' ta có: BH = d (B, DB').
Xét tam giác BB'D vuông tại B ta có:
2. Khoảng cách từ một điểm đến một mặt phẳng
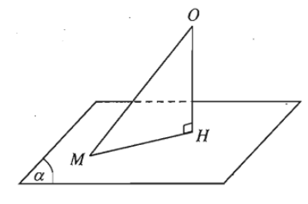
Cho điểm O và mặt phẳng (α). Gọi H là hình chiếu vuông góc của O lên mặt phẳng (α). Khi đó khoảng cách giữa hai điểm O và H được gọi là khoảng cách từ điểm O đến mặt phẳng (α) và được kí hiệu là d(O; (α)).
Ví dụ 2. Cho hình chóp S. ABC có , ∆ABC là tam giác đều cạnh a và tam giác SAB cân. Tính khoảng cách h từ điểm A đến mặt phẳng (SBC).
Lời giải:
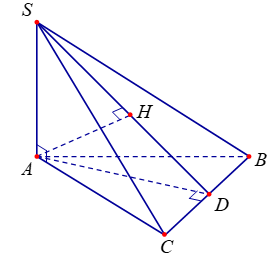
Gọi D là trung điểm BC. Do tam giác ABC đều nên (1).
Trong tam giác SAD, kẻ (2).
Do (3).
Từ (2) và (3), ta suy ra AH vuông góc với (SBC) nên d(A ; (SBC))= AH.
Theo giả thiết, ta có SA = AB = a, (đường cao trong tam giác đều cạnh a).
Tam giác SAD vuông nên
II. Khoảng cách giữa đường thẳng và mặt phẳng song song, giữa hai mặt phẳng song song.
1. Khoảng cách giữa đường thẳng và măt phẳng song song.
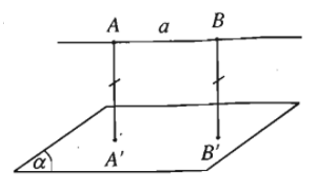
- Định nghĩa: Cho đường thẳng a song song với mặt phẳng (α). Khoảng cách giữa đường thẳng a và mặt phẳng (α) là khoảng cách từ một điểm bất kì thuộc a đến mặt phẳng (α).
Kí hiệu là d(a; (α)) .
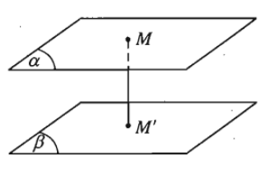
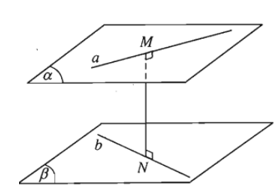
2. Khoảng cách giữa hai mặt phẳng song song.
- Định nghĩa: Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm bất kì của mặt phẳng này đến mặt phẳng kia.
- Kí hiệu: d((α); (β)).
Như vậy: d((α); (β)) = d(M; (β)) = d(M’; (α)).
III. Đường vuông góc chung và khoảng cách hai đường thẳng chéo nhau.
1. Định nghĩa.
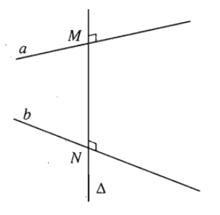
a) Đường thẳng ∆ cắt hai đường thẳng chéo nhau a, b và cùng vuông góc với mỗi đường thẳng ấy được gọi là đường vuông góc chung của a và b.
b) Nếu đường vuông góc chung ∆ cắt hai đường thẳng chéo nhau a, b lần lượt tại M; N thì độ dài đoạn thẳng MN gọi là khoảng cách giữa hai đường thẳng chéo nhau a và b.
2. Cách tìm đường vuông góc chung của hai đường thẳng chéo nhau.
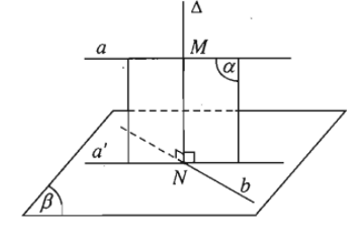
- Cho hai đường thẳng chéo nhau a và b. Gọi (β) là mặt phẳng chứa b và song song với a; a’ là hình chiếu vuông góc của a trên mặt phẳng (β).
Vì a// (β) nên a// a’. Do đó; a’ cắt b tại 1 điểm là N
Gọi (α) là mặt phẳng chứa a và a’; ∆ là đường thẳng đi qua N và vuông góc với (β). Khi đó, (α) vuông góc (β).
Như vậy.∆ nằm trong (α) nên cắt đường thẳng a tại M và cắt đường thẳng b tại N.Đồng thời, ∆ vuông góc với cả a và b.
Do đó, ∆ là đường vuông góc chung của a và b.
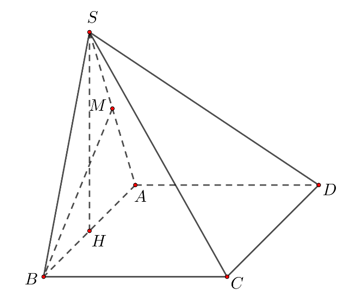
Ví dụ 3. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng chéo nhau SA và BC.
Lời giải :
Do và .
Vì tam giác SAB đều nên gọi M là trung điểm của SA thì nên BM là đoạn vuông góc chung của BC và SA.
Vậy .
3. Nhận xét
a) Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa một trong hai đường thẳng đó đến mặt phẳng song song với nó và chứa đường thẳng còn lại.
b) Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đó.
Ví dụ 4. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy, SA= a. Khoảng cách giữa hai đường thẳng SB và CD là
Lời giải :
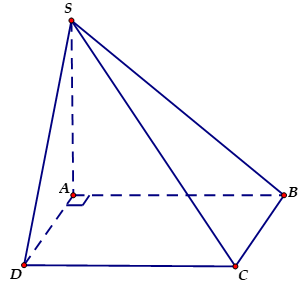
Vì .
Ta có:
Vì
Suy ra: CD // (SAB) nên :
d(CD, SB) = d(CD, (SAB)) = d(D, (SAB)) = DA = a,