Khẳng định nào sau đây là đúng?
A. nếu mặt phẳng (P) chứa hai đường thẳng cùng song song với mặt phẳng (Q) thì (P) // (Q).
B. nếu hai đường thẳng cùng nằm trong một mặt phẳng lần lượt song song với hai đường thẳng của một mặt phẳng khác thì hai mặt phẳng đó song song.
C. hai mặt phẳng cùng song song với mặt phẳng thứ ba thì song song với nhau
D. cho hai mặt phẳng (P) , (Q) song song. Khi đó nếu đường thẳng a không nằm trong mặt phẳng (Q) và a song song với (P) thì a song song với (Q)
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình lăng trụ ABC.A’B’C’. gọi I, J, K lần lượt là trọng tâm của các tam giác ABC, ACC’, A’B’C’. mặt phẳng nào sau đây song song với (IJK)?
Cho hai mặt phẳng (∝), (β) cắt nhau và cùng song song với đường thẳng d. Khẳng định nào sau đây là đúng?
Trong các mệnh đề sau, những mệnh đề nào đúng?
(1) hai mặt phẳng phân biệt cùng song song với một đường thẳng thì song song với nhau.
(2) hai mặt phẳng phân biệt không song song thì cắt nhau.
(3) hai mặt phẳng cùng song song với một mặt phẳng thứ ba thì song song với nhau.
(4) Một đường thẳng cắt một trong hai mặt phẳng song song thì cắt mặt phẳng còn lại.
Cho hai hình bình hành ABCD và ABEF có tâm lần lượt là O, O’ và không cùng nằm trong một mặt phẳng. gọi M là trung điểm của AB.
(I) (ADF) // (BCE) (II) (MOO’) // (ADF)
(III) (MOO’) // (BCE) (IV) (AEC) // (BDF)
Khẳng định nào sau đây là đúng
Cho mặt phẳng (R) cắt hai mặt phẳng song song (P) và (Q) theo hai giao tuyến a và b. Khi đó.
Cho hai mặt phẳng phân biệt (P) và (Q)
(1) nếu hai mặt phẳng (P) và (Q) song song với nhau thì mọi đường thẳng nằm trên (P) đều song song với mọi đường thẳng nằm trên (Q).
(2) nếu mọi đường thẳng nằm trong mặt phẳng (P) đều song song với (Q) thì (P) song song với (Q).
Trong hai phát biểu trên.
Cho hai đường thẳng chéo nhau a và b. (P) chứa a và song song với b, Q chứa b và song song với a. Phát biểu nào sau đây là đúng?
Cho hình bình hành ABCD. Qua các đỉnh A, B, C, D ta dựng các nửa đường thẳng song song với nhau và nằm về một phía đối với mặt phẳng (ABCD). Một mặt phẳng (P) cắt bốn đường thẳng nói trên tại A’, B’, C’, D’. Hỏi A’B’C’D’ là hình gì?
Cho hai đường thẳng a và b lần lượt nằm trên hai mặt phẳng song song (P) và (Q). Chọn mệnh đề đúng
Cho hình bình hành ABCD. Gọi Bx, Cy, Dz là các đường thẳng đi qua B, C, D và song song với nhau. Mặt phẳng (∝) đi qua A và cắt Bx, Cy, Dz lần lượt tại B’, C’, D’ với BB’ = 2, DD’ = 4. Khi đó CC’ bằng:
Cho tứ diện đều S.ABC. Gọi I là trung điểm của AB, M là một điểm lưu động trên đoạn AI. Qua M vẽ mặt phẳng (∝) //(SIC). Khi đó thiết diện của mặt phẳng (∝) và tứ diện S.ABC là:
I. Định nghĩa
Hai mặt phẳng (α), (β) được gọi là song song với nhau nếu chúng không có điểm chung.
Khi đó ta kí hiệu (α) // (β) hoặc (β) // (α).
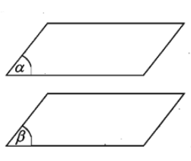
II. Tính chất
- Định lí 1. Nếu mặt phẳng (α) chứa hai đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng (β) thì (α) song song với (β).
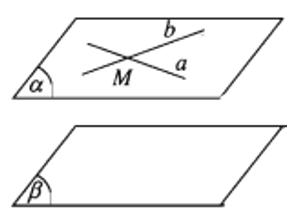
Ta có:
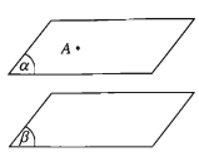
- Định lí 2. Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chỉ một mặt phẳng song song với mặt phẳng đã cho.
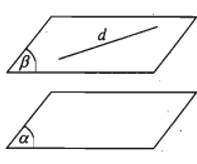
- Hệ quả 1. Nếu đường thẳng d song song với mặt phẳng (α) thì qua d có duy nhất một mặt phẳng song song với (α).
- Hệ quả 2. Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì song song với nhau.
- Hệ quả 3. Cho điểm A không nằm trên mặt phẳng (α). Mọi đường thẳng đi qua A và song song với (α) đều nằm trong mặt phẳng đi qua A và song song với (α).
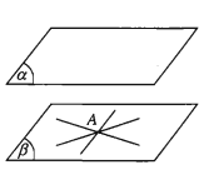
- Định lí 3. Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.
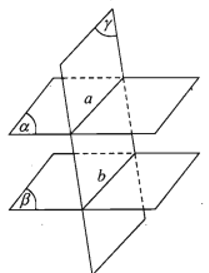
- Hệ quả. Hai mặt phẳng song song chắn trên hai cát tuyến song song những đoạn thẳng bằng nhau.
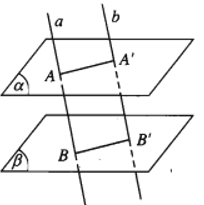
Ví dụ 1. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P theo thứ tự là trung điểm của SA, SD và AB. Chứng minh:
a) M, N, O, P đồng phẳng.
b) mp(MON) // mp(SBC).
Lời giải:
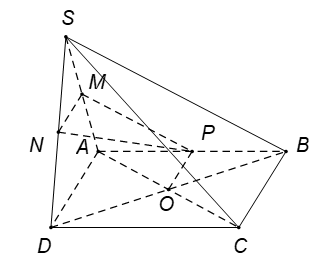
a) Ta có MN là đường trung bình của tam giác SAD nên MN // AD (1).
Và OP là đường trung bình của tam giác ABC nên OP // BC // AD (2).
Từ (1) và (2) suy ra MN // OP // AD nên 4 điểm M, N, O, P đồng phẳng.
b) Vì
Suy ra, (MNOP) // (SBC) hay (MON) // (SBC).
Ví dụ 2. Cho hình hộp ABCD.A’B’C’D’. Gọi I là trung điểm của A’B’. Mặt phẳng (IBD) cắt hình hộp theo thiết diện là hình gì?
Lời giải:
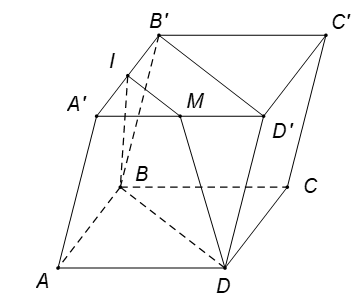
- Ta tìm giao tuyến của 2 mp(IBD) và (A’B’C’D’)
Suy ra, giao tuyến của (IBD) với (A’B’C’D’) là đường thẳng d đi qua I và song song với BD.
- Trong mặt phẳng (A’B’C’D’), gọi M là giao điểm của d và A’D’.
Suy ra, IM // BD // B’D’.
Khi đó thiết diện là tứ giác IMDB và tứ giác này là hình thang.
III. Định lí Ta – let (Thalès)
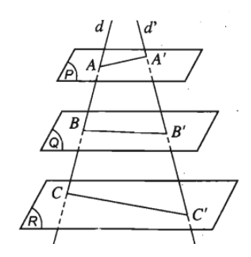
- Định lí 4 (định lí Ta- let). Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì những đoạn thẳng tương ứng tỉ lệ.
- Nếu d, d’ là hai cát tuyến bất kì cắt ba mặt phẳng song song (α), (β), lần lượt tại các điểm A, B, C và A’, B’, C’ thì:
IV. Hình lăng trụ, hình hộp
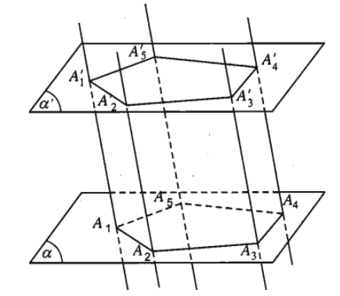
Cho hai mặt phẳng song song (α) và (α’). Trên (α) cho đa giác lồi A1A2…An. Qua các đỉnh A1, A2,.., An ta vẽ các đường thẳng song song với nhau và cắt (α’) lần lượt tại .
Hình gồm hai đa giác A1A2…An, và các hình bình hành A1A1’A2’A2;
A2A2’A3’A3,…, AnAn’A1’A1 được gọi là hình lăng trụ và được kí hiệu là A1A2…An. .
- Hai đa giác A1A2…An, gọi là hai mặt đáy của hình lăng trụ.
- Các đoạn thẳng A1A’1, A2A2’,…., AnAn’ gọi là các cạnh bên của hình lăng trụ.
- Các hình bình hành A1A1’A2’A2, A2A2’A3’A3, …, AnAn’A1’A1 được gọi là các mặt bên của hình lăng trụ.
- Các đỉnh của hai đa giác được gọi là các đỉnh của hình lăng trụ.
- Nhận xét:
+ Các cạnh bên của hình lăng trụ bằng nhau và song song với nhau.
+ Các mặt bên của hình lăng trụ là các hình bình hành.
+ Hai mặt đáy của hình lăng trụ là hai đa giác bằng nhau.
Người ta gọi tên của hình lăng trụ dựa vào tên của đa giác đáy, chẳng hạn:
+ Hình lăng trụ có đáy là hình tam giác được gọi là hình lăng trụ tam giác.
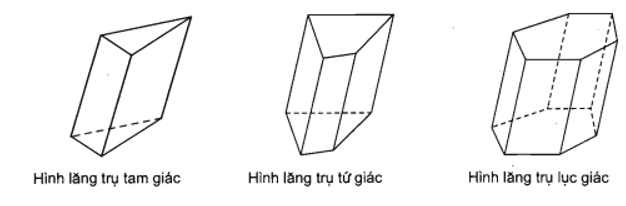
+ Hình lăng trụ có đáy là hình bình hành được gọi là hình hộp.
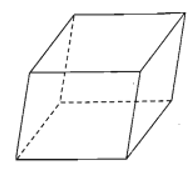
V. Hình chóp cụt
Định nghĩa:
Cho hình chóp S.A1A2…An ; một mặt phẳng (P) không qua đỉnh, song song với mặt phẳng đáy của hình chóp cắt các cạnh SA1, SA2, …,SAn lần lượt tại A1’; A2’,.., An’. Hình tạo bởi thiết diện A1’A2’..An’ và đáy A1A2…An của hình chóp cùng với các tứ giác A1A1’A2’A2, A2A2’A3’A3,…, AnAn’A1’A1 gọi là hình chóp cụt.
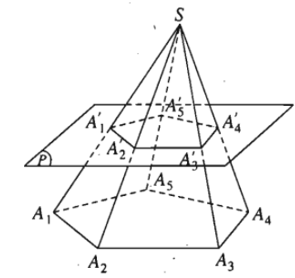
Đáy của hình chóp gọi là đáy lớn của hình chóp cụt, còn thiết diện A1’A2’..An’ gọi là đáy nhỏ của hình chóp cụt.
Các tứ giác A1A1’A2’A2, A2A2’A3’A3,…, AnAn’A1’A1 gọi là các mặt bên của hình chóp cụt.
Các đoạn thẳng A1A’1, A2A2’,…., AnAn’ gọi là các cạnh bên của hình chóp cụt.
- Tính chất của hình chóp cụt
(1) Hai đáy là hai đa giác có các cạnh tương ứng song song và các tỉ số các cặp cạnh tương ứng bằng nhau.
(2) Các mặt bên là những hình thang.
(3) Các đường thẳng chứa các cạnh bên đồng quy tại một điểm.