Cho lục giác đều ABCDEF nội tiếp trong đường tròn lượng giác (thứ tự đi từ A đến các đỉnh theo chiều ngược chiều kim đồng hồ). Tính số đo của các góc lượng giác (OA, OB), (OA, OC), (OA, OD), (OA, OE), (OA, OF).
 Giải bởi Vietjack
Giải bởi Vietjack
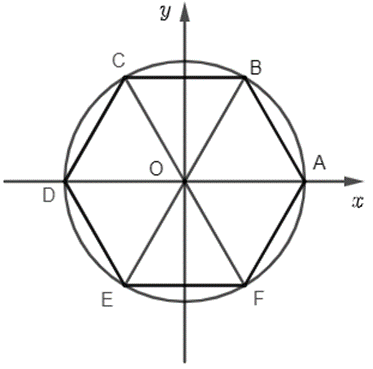
Vì ABCDEF là lục giác đều nên
\(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \widehat {FOA} = \frac{{360^\circ }}{6} = 60^\circ = \frac{\pi }{3}\).
Khi đó, ta có:
\(\left( {OA,OB} \right) = \frac{\pi }{3} + k2\pi \);
\(\left( {OA,OC} \right) = \frac{\pi }{3} + \frac{\pi }{3} + k2\pi = \frac{{2\pi }}{3} + k2\pi \);
\(\left( {OA,OD} \right) = \pi + k2\pi \);
\(\left( {OA,OE} \right) = - \frac{\pi }{3} - \frac{\pi }{3} + k2\pi = - \frac{{2\pi }}{3} + k2\pi \);
\(\left( {OA,OF} \right) = - \frac{\pi }{3} + k2\pi \).
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Một vòng quay Mặt Trời quay mỗi vòng khoảng 15 phút. Tại vị trí quan sát, bạn Linh thấy vòng quay chuyển động theo chiều kim đồng hồ. Khi vòng quay chuyển động được 10 phút, bán kính của vòng quay quét một góc lượng giác có số đo bằng bao nhiêu? (Tính theo đơn vị radian).
Chứng minh rằng trong tam giác ABC, ta có:
\(\tan \frac{{A + B - 2C}}{2} = \cot \frac{{3C}}{2}\).
Cho sin α + cos α = \(\frac{1}{3}\) với \( - \frac{\pi }{2} < \alpha < 0\). Tính:
C = sin³ α + cos³ α;
Tính:
B = \(\sin \frac{\pi }{5} + \sin \frac{{2\pi }}{5} + ... + \sin \frac{{9\pi }}{5}\) (gồm 9 số hạng);
Cho sin α + cos α = \(\frac{1}{3}\) với \( - \frac{\pi }{2} < \alpha < 0\). Tính:
B = sin α – cos α;
Cho tan x = − 2. Tính giá trị của biểu thức sau:
\(B = \frac{{2{{\sin }^2}x - 3\sin x\cos x - {{\cos }^2}x}}{{{{\sin }^2}x + \sin x\cos x}}\).
Chứng minh rằng trong tam giác ABC, ta có:
\(\sin \frac{A}{2} = \cos \frac{{B + C}}{2}\);
Cho sin α + cos α = \(\frac{1}{3}\) với \( - \frac{\pi }{2} < \alpha < 0\). Tính:
D = sin4 α + cos4 α.
Cho \(\sin \alpha = \frac{1}{3}\) với \(\alpha \in \left( {\frac{\pi }{2};\pi } \right)\). Tính cos α, tanα, cot α.
Tính:
C = tan 1° . tan 2° . tan 3°. ... . tan 89° (gồm 89 thừa số).
Cho sin α + cos α = \(\frac{1}{3}\) với \( - \frac{\pi }{2} < \alpha < 0\). Tính:
A = sinα . cos α;
Tính:
A = \({\cos ^2}\frac{\pi }{8} + {\cos ^2}\frac{{3\pi }}{8} + {\cos ^2}\frac{{5\pi }}{8} + {\cos ^2}\frac{{7\pi }}{8}\);