Một nguồn phát sóng dao động điều hòa tạo ra sóng tròn đồng tâm \(O\) truyền trên mặt nước với bước sóng \(\lambda \). Hai điểm \(M\) và \(N\) thuộc mặt nước, nằm trên hai phương truyền sóng mà các phần tử nước đang dao động. Biết \(OM = 8\lambda ,ON = 12\lambda \) và \(OM\) vuông góc với \(ON\). Trên đoạn \(MN\), số điểm mà phần tử nước dao động ngược pha với dao động của nguồn \(O\) là
 Giải bởi Vietjack
Giải bởi Vietjack
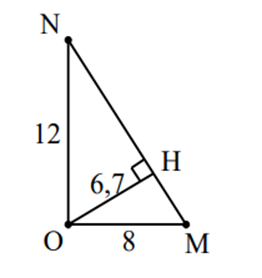
+ Kẻ OH vuông góc với MN áp dụng hệ thức trong tam giác vuông có:
\(\frac{1}{{O{H^2}}} = \frac{1}{{O{M^2}}} + \frac{1}{{O{N^2}}} = \frac{1}{{{{(8\lambda )}^2}}} + \frac{1}{{{{(12\lambda )}^2}}} \Rightarrow OH \approx 6,7\lambda \)
+ Dễ thấy: Một điểm bất kì thuộc MN dao động ngược pha với nguồn O thỏa mãn điều kiện khoảng cách tới nguồn O bằng số bán nguyên lần bước sóng.
+ Trên MH có 1 điểm ngược pha với O có \(d = 7,5\lambda \)
+ Trên NH có các điểm ngược pha với nguồn có khoảng cách lần lượt \(d = 7,5\lambda ;\,\,8,5\lambda ;\,\,9,5\lambda ;\,\,10,5\lambda ;\,\,11,5\lambda \); Có tổng cộng 5 điểm trên NH ngược pha với nguồn.
+ Vậy trên MN có 5 + 1 = 6 điểm ngược pha với nguồn O. Chọn đáp án \[D.\]
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Một con lắc đơn có chiều dài 1 dao động điều hòa với biên độ góc \({\alpha _0}\) tại nơi có gia tốc trọng trường g. Ở thời điểm t vật có tốc độ v, lúc đó vật có li độ góc là
Một con lắc lò xo gồm vật có khối lượng m và lò xo có độ cứng k, dao động điều hòa. Nếu tăng độ cứng \(k\) lên 2 lần và giảm khối lượng \(m\) đi 8 lần thì tần số dao động của vật sẽ
Con lắc lò xo đặt nằm ngang, ban đầu lò xo chưa bị biến dạng, vật có khối lượng \({m_1} = 0,5\;kg\) lò xo có độ cứng \(k = 20\;N/m\). Một vật có khối lượng \({m_2} = 0,5\;kg\) chuyển động dọc theo trục của lò xo với tốc độ \(0,2\sqrt {22} \;m/s\) đến va chạm mềm với vật \({m_1}\) sau va chạm lò xo bị nén lại. Hệ số ma sát trượt giữa vật và mặt phẳng nằm ngang là 0,1 lấy \(g = 10\;m/{s^2}\). Tốc độ cực đại của vật sau lần nén thứ nhất là
Một con lắc đơn có chiều dài \(0,5(\;m)\), quả cầu nhỏ có khối lượng 200 (\(g\)), dao động tại nơi có gia tốc trọng trường \(9,8\;m/{s^2}\), với biên độ góc 0,12 (rad). Trong quá trình dao động, con lắc luôn chịu tác dụng lực ma sát nhỏ có độ lớn không đổi \(0,002(\;N)\) thì nó sẽ dao động tắt dần. Tính tổng quãng đường quả cầu đi được từ lúc bắt đầu dao động cho đến khi dừng hẳn.
Một vật dao động điều hòa có độ lớn vận tốc cực đại là \(31,4\;cm/s\). Lấy \(\pi = 3,14\). Tốc độ trung bình của vật trong một chu kì dao động là
Một con lắc đơn có chiều dài \(1(\;m)\), khối lượng \(m\). Kéo con lắc khỏi vị trí cân bằng một góc 0,1 (rad) và thả cho dao động không vận tốc đầu. Khi chuyền động qua vị trí cân bằng và sang phía bên kia con lắc va chạm đàn hồi với mặt phẳng cố định đi qua điểm treo, góc nghiêng của mặt phẳng và phương thẳng đứng là \(0,05\sqrt 2 (rad)\). Lấy gia tốc trọng trường \(g = {\pi ^2} = 9,85\left( {\;m/{s^2}} \right)\), bỏ qua ma sát. Chu kì dao động của con lắc là
Ba lò xo có cùng chiều dài tự nhiên có độ cứng lần lượt là \({k_1},{k_2},{k_3}\), đầu trên treo vào các điểm cố định, đầu dưới treo vào các vật có cùng khối lượng. Lúc đầu, nâng ba vật đến vị trí mà các lò xo không biến dạng rồi thả nhẹ đề chúng dao động điều hòa với cơ năng lần lượt là \({W_1} = 0,1\;J,\;{W_2} = 0,2\;J\) và \({W_3}\). Nếu \({k_3} = 2,5{k_1} + 3{k_2}\) thì \({W_3}\) bằng
Ở mặt nước có hai nguồn sóng dao động theo phương vuông góc với mặt nước, có cùng phương trình \(u = Acos\omega t\). Trong miền gặp nhau của hai sóng, những điểm mà ở đó các phần tử nước dao động với biên độ cực đại sẽ có hiệu đường đi của sóng từ hai nguồn đến đó bằng
Ở mặt thoáng của một chất lỏng có hai nguồn sóng kết hợp \(A\) và \(B\) cách nhau \(20\;cm\), dao động theo phương thẳng đứng với phương trình \({u_A} = 2\cos 40\pi t\) và \({u_B} = 2\cos (40\pi t + \pi )\left( {{u_A}} \right.\) và \({u_B}\) tính bằng mm, \(t\) tính bằng s). Biết tốc độ truyền sóng trên mặt chất lỏng là \(30\;cm/s\). Xét hình vuông \(AMNB\) thuộc mặt thoáng chất lỏng. Số điểm dao động với biên độ cực đại trên đoạn BM là
Một con lắc đơn dao động điều hoà tại một nơi có \(g = 9,8\;m/{s^2}\). Vận tốc cực đại của dao động 39,2 \(cm/s\). Khi vật đi qua vị trí có li độ dài \(s = 3,92\;cm\) thì có vận tốc \(19,6\sqrt 3 \;cm/s\). Chiều dài dây treo vật là